《2025年学习检测九年级数学上册华师大版河南专版》

17. “五一”期间,小明与爸爸妈妈去上海游玩,当小明从一塔形建筑物边经过时,建筑物的影子清晰地映在地面上.小明想估计一下这座建筑物的高度,但身上未带任何测量工具,于是他灵机一动,利用自己的身高和脚长就解决了这个问题.你知道他是怎样解决的吗？(已知相同时刻物高与影长成比例)

答案： 用脚估算出塔形建筑物的影长与自己的影长.再由同一时刻物高与影长成比例,得$\frac{建筑物的影长}{建筑物的高}=\frac{自己的影长}{自己的身高}$,即可求出建筑物的高度.

1. 如果 $ x:y = 2:3 $,则下列各式不成立的是 【D】
A.$ \frac{x + y}{y} = \frac{5}{3} $
B.$ \frac{y - x}{y} = \frac{1}{3} $
C.$ \frac{x}{2y} = \frac{1}{3} $
D.$ \frac{x + 1}{y + 1} = \frac{3}{4} $

答案： D.

2. 已知线段 $ a $、$ b $、$ c $,求作线段 $ x $ 使 $ \frac{a}{b} = \frac{c}{x} $,下列作法(图中虚线均为平行线)中不正确的是 【D】

答案： D.

3. 直线 $ l_1 // l_2 // l_3 $,另两条直线分别交 $ l_1 $、$ l_2 $、$ l_3 $ 于点 $ A $、$ B $、$ C $ 及点 $ D $、$ E $、$ F $,且 $ AB = 3 $,$ DE = 4 $,$ EF = 2 $,则 【D】
A.$ BC:DE = 1:2 $
B.$ BC:DE = 2:3 $
C.$ BC \cdot DE = 8 $
D.$ BC \cdot DE = 6 $

答案： D.

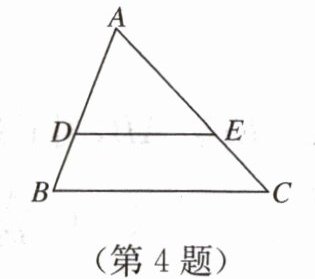
4. 如图,$ ED // BC $,$ AB = 14 $,$ AC = 18 $,$ AE = 10 $,则 $ AD = $$7\frac{7}{9}$。
]

答案： $7\frac{7}{9}.$