《2025年学习检测九年级数学上册华师大版河南专版》

1. 已知两个相似多边形的相似比为$1:2$,则它们的周长比为$1:2$,面积比为$1:4$.

答案： $1:2,1:4$.

2. 如图①是伸缩折叠不锈钢晾衣架的实物图,图②是它的侧面示意图,$AD与CB相交于点O$,$AB// CD$,根据图②中的数据,可得$x$的值为1.2.

答案： 1.2.

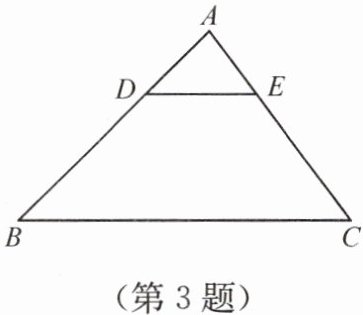
3. 如图,在$\triangle ABC$中,$DE// BC$,$AD = \frac{1}{3}BD$,则$DE:BC = $$1:4$,$S_{\triangle ADE}:S_{\triangle ABC} = $$1:16$.

答案： $1:4,1:16$.

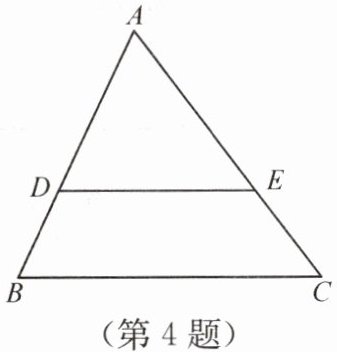
4. 如图,在$\triangle ABC$中,$DE// BC$,$S_{\triangle ADE} = S_{四边形BCED}$,则$AD:AB = $$1:\sqrt {2}$.

答案： $1:\sqrt {2}$.

5. 如图,在$\triangle ABC$中,$DE// BC$,$AD:AB = 2:3$,则$S_{\triangle ADE}:S_{\triangle ABC} = $$4:9$.

答案： $4:9$.

6. 如图,若$AB// CD$,$OC:AC = 1:3$,则$S_{\triangle OCD}:S_{\triangle OAB} = $$1:4$.

答案： $1:4$

7. 如图,在$\triangle ABC$中,$D是AB$上一点,$DE// BC交AC于点E$,且$DE把\triangle ABC分成两个部分的面积之比为4:5$,求$\frac{AE}{AC}$.

答案： 若$S_{\triangle ADE}:$$S_{四边形DBCE}=4:5$,则$S_{\triangle ADE}:S_{\triangle ABC}=4:9$.又$\because DE// BC$,$\therefore \triangle ADE\backsim \triangle ABC$.$\therefore (\frac {AE}{AC})^{2}=\frac {4}{9}$.$\therefore \frac {AE}{AC}=\frac {2}{3}$;若$S_{\triangle ADE}:S_{四边形DBCE}=5:4$,则有$(\frac {AE}{AC})^{2}=\frac {5}{9}$,$\therefore \frac {AE}{AC}=\frac {\sqrt {5}}{3}$,故$\frac {AE}{AC}=\frac {2}{3}$或$\frac {\sqrt {5}}{3}$.