《2025年学习检测九年级数学上册华师大版河南专版》

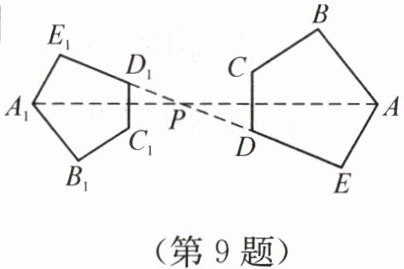
9. 如图,五边形$ABCDE和五边形A_1B_1C_1D_1E_1$是位似图形,且$PA_1= \frac{2}{3}PA$,则$AB:A_1B_1$等于【B】

A.$\frac{2}{3}$
B.$\frac{3}{2}$
C.$\frac{3}{5}$
D.$\frac{5}{3}$

答案： B

10. 一般在室外放映的电影胶片上每一个图片的规格为$3.5\mathrm{cm}×3.5\mathrm{cm}$,放映银幕的规格为$2\mathrm{m}×2\mathrm{m}$,若影机的光源距胶片$20\mathrm{cm}$,为使放映的影像刚好布满整个银幕,则银幕应拉在光源外【C】
A.$2\mathrm{m}$处
B.$3.5\mathrm{m}$处
C.$\frac{80}{7}\mathrm{m}$处
D.$\frac{8000}{7}\mathrm{m}$处

答案： C

11. 在$\triangle ABC$中,$BC = 30$,$AC = 20$,$AB = 15$.将$\triangle ABC$缩小后,得到的三角形的最短边为$3$,则缩小后的三角形的周长为13.

答案： 13

12. 如图,$\triangle OAB与\triangle OCD$是位似图形,$AB与CD$平行吗？为什么？

答案： 平行.
∵△OAB 与△OCD 是位似图形，
∴△OAB∽△OCD，
∴∠A=∠C，
∴AB//CD(同位角相等，两直线平行).

13. 如图,用下面的方法可以画$\triangle AOB$的内接等边三角形.
画法：①在$\triangle AOB内画等边三角形CDE$,使点$C在OA$上,点$D在OB$上；②连结$OE$并延长,交$AB于点E'$,过点$E'作E'C'// EC$,交$OA于点C'$,作$E'D'// ED$,交$OB于点D'$；③连结$C'D'$,则$\triangle C'D'E'是\triangle AOB$的内接三角形.
求证：$\triangle C'D'E'$是等边三角形.

答案：
∵EC//E'C'，
∴$\frac{CE}{C'E'}=\frac{OE}{OE'}$，∠CEO=∠C'E'O.
∵ED//E'D'，
∴$\frac{ED}{E'D'}=\frac{OE}{OE'}$，∠DEO=∠D'E'O，
∴∠CED=∠C'E'D'=60°，又
∵$\frac{CE}{C'E'}=\frac{ED}{E'D'}$，
∴△CED∽△C'E'D'，
∴△C'E'D'是等边三角形.