《2025年学习检测九年级数学上册华师大版河南专版》

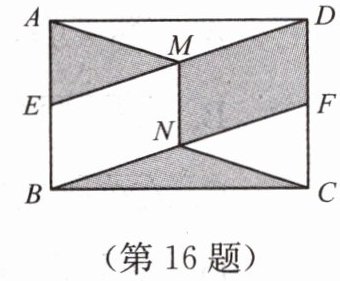
16. 如图,在矩形$ABCD$中,点$E$、$F分别是AB$、$CD$的中点,连结$DE和BF$,分别取$DE$、$BF的中点M$、$N$,连结$AM$、$CN$、$MN$。若$AB = 2\sqrt{2}$,$BC = 2\sqrt{3}$,求图中阴影部分的面积。

答案： $S_{阴影}=\frac{1}{2}S_{矩形ABCD}=\frac{1}{2}× 2\sqrt{2}× 2\sqrt{3}=2\sqrt{6}$

1. 化简$\sqrt{x^{4}y + x^{2}y^{4}}(x＞0)$的结果是 【B】
A.$x^{2}y\sqrt{1 + y^{2}}$
B.$x\sqrt{x^{2}y + y^{4}}$
C.$xy\sqrt{x^{2} + y^{2}}$
D.$x^{2}\sqrt{y + y^{4}}$

答案： B

2. 下列各式中,计算正确的是 【C】
A.$\sqrt{(-25)(-4)} = \sqrt{-25} \cdot \sqrt{-4}$
B.$\sqrt{5^{2} + 3^{2}} = 5 + 3 = 8$
C.$\sqrt{(-2)^{2}×25} = \sqrt{(-2)^{2}} \cdot \sqrt{25} = 10$
D.$\sqrt{15^{2} - 14^{2}} = 15 - 14 = 1$

答案： C

3. 若$\sqrt{a(a - 2)} = \sqrt{a} \cdot \sqrt{a - 2}$成立,则$a$的取值范围是 【B】
A.$a \geq 0$
B.$a \geq 2$
C.$0 \leq a \leq 2$
D.一切实数

答案： B

4. 对于任意实数$x$,下列各式中一定成立的是 【D】
A.$\sqrt{x^{2} - 1} = \sqrt{x - 1} \cdot \sqrt{x + 1}$
B.$\sqrt{(x + 1)^{2}} = x + 1$
C.$\sqrt{(-4) \cdot (-x)} = \sqrt{-4} \cdot \sqrt{-x}$
D.$\sqrt{36x^{4}} = 6x^{2}$

答案： D

5. 已知$x^{2}y ＜ 0$,化简二次根式$\sqrt{-xy^{2}}$的结果是$-y\sqrt{-x}$。

答案： $-y\sqrt{-x}$

6. 化简：(1) $\sqrt{18} = $$3\sqrt{2}$； (2) $\sqrt{54} = $$3\sqrt{6}$；
(3) $\sqrt{3a^{2}b^{2}}(a＞0,b＜0)= $$-\sqrt{3}ab$； (4) $\sqrt{36(x - y)^{3}}(x＞y)= $$6(x-y)\sqrt{x-y}$。

答案：
(1)$3\sqrt{2}$;
(2)$3\sqrt{6}$;
(3)$-\sqrt{3}ab$;
(4)$6(x-y)\sqrt{x-y}$

7. 计算：
(1) $\sqrt{\frac{9}{4}×\frac{144}{81}}$； (2) $\sqrt{(-3)^{2}×(-7)^{2}}$。

答案：
(1)2;
(2)21