第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
5. 某窗户的形状如图所示(图中长度单位:cm),其中上部分是半径为 $ x $ cm 的半圆形,下部分是长为 $ y $ cm 的长方形.
(1) 用含 $ x $,$ y $ 的式子表示窗户的面积 $ S $;
(2) 当 $ x = 40 $,$ y = 120 $ 时,求窗户的面积 $ S $.

(1) 用含 $ x $,$ y $ 的式子表示窗户的面积 $ S $;
(2) 当 $ x = 40 $,$ y = 120 $ 时,求窗户的面积 $ S $.

答案:
5.
(1)解:由图可得,$S=\frac {1}{2}πx^{2}+2x\cdot y=\frac {1}{2}πx^{2}+2xy$,即窗户的面积S是$(\frac {1}{2}πx^{2}+2xy)cm^{2}$;
(2)当$x=40,y=120$时,$S=\frac {1}{2}π×40^{2}+2×40×120=800π+9600$,即当$x=40,y=120$时,窗户的面积S是$(800π+9600)cm^{2}$.
(1)解:由图可得,$S=\frac {1}{2}πx^{2}+2x\cdot y=\frac {1}{2}πx^{2}+2xy$,即窗户的面积S是$(\frac {1}{2}πx^{2}+2xy)cm^{2}$;
(2)当$x=40,y=120$时,$S=\frac {1}{2}π×40^{2}+2×40×120=800π+9600$,即当$x=40,y=120$时,窗户的面积S是$(800π+9600)cm^{2}$.
6. 如图,某学校设计在长为 $ y $ 米,宽为 36 米的大长方形场地中,并排新建三个大小一样的标准篮球场,三个篮球场之间及篮球场与长方形场地边沿的距离均为 $ a $ 米,篮球场的宽为 $ b $ 米.
(1) 用含 $ a $,$ b $ 的代数式表示一个篮球场的周长;
(2) 若 $ |a - 4| + (b - 15)^2 = 0 $,求整个场地的面积.

(1) 用含 $ a $,$ b $ 的代数式表示一个篮球场的周长;
(2) 若 $ |a - 4| + (b - 15)^2 = 0 $,求整个场地的面积.

答案:
6.
(1)解:一个篮球场的周长为$2(36-2a+b)=(72-4a+2b)$(米),即一个篮球场的周长为$(72-4a+2b)$米;
(2)因为$|a-4|+(b-15)^{2}=0$,所以$a-4=0,b-15=0$,即$a=4,b=15$,则$36(4a+3b)=36×(4×4+3×15)=2196$(平方米),即整个场地的面积为2196平方米.
(1)解:一个篮球场的周长为$2(36-2a+b)=(72-4a+2b)$(米),即一个篮球场的周长为$(72-4a+2b)$米;
(2)因为$|a-4|+(b-15)^{2}=0$,所以$a-4=0,b-15=0$,即$a=4,b=15$,则$36(4a+3b)=36×(4×4+3×15)=2196$(平方米),即整个场地的面积为2196平方米.
7. 如图所示,将面积为 $ a^2 $ 的小正方形和面积为 $ b^2 $ 的大正方形放在同一水平面上($ b > a > 0 $).
(1) 用 $ a $,$ b $ 表示阴影部分的面积;
(2) 计算当 $ a = 3 $,$ b = 5 $ 时,阴影部分的面积.
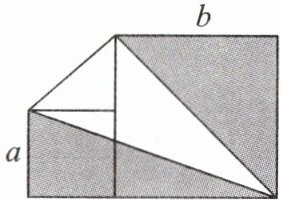
(1) 用 $ a $,$ b $ 表示阴影部分的面积;
(2) 计算当 $ a = 3 $,$ b = 5 $ 时,阴影部分的面积.

答案:
7.
(1)解:阴影部分的面积为$\frac {1}{2}b^{2}+\frac {1}{2}a(a+b)$.
(2)当$a=3,b=5$时,$\frac {1}{2}b^{2}+\frac {1}{2}a(a+b)=\frac {1}{2}×25+\frac {1}{2}×3×(3+5)=\frac {49}{2}$,即阴影部分的面积为$\frac {49}{2}$.
(1)解:阴影部分的面积为$\frac {1}{2}b^{2}+\frac {1}{2}a(a+b)$.
(2)当$a=3,b=5$时,$\frac {1}{2}b^{2}+\frac {1}{2}a(a+b)=\frac {1}{2}×25+\frac {1}{2}×3×(3+5)=\frac {49}{2}$,即阴影部分的面积为$\frac {49}{2}$.
8. (方案选择)某中学七年级(4)班三位教师决定带领本班 $ a $ 名学生(学生人数不少于 3 人),在五一期间去北京旅游,甲旅行社的收费标准为:教师全价,学生半价;而乙旅行社不分教师、学生一律八折优惠.这两家旅行社的基本价都是 500 元.
(1) 用含 $ a $ 的代数式表示这三位教师和 $ a $ 名学生分别参加这两家旅行社所需的总费用;
(2) 当 $ a = 6 $ 时,你认为选择哪一家旅行社较为合算,为什么?
(1) 用含 $ a $ 的代数式表示这三位教师和 $ a $ 名学生分别参加这两家旅行社所需的总费用;
(2) 当 $ a = 6 $ 时,你认为选择哪一家旅行社较为合算,为什么?
答案:
8.
(1)解:甲旅行社的收费为$500×3+\frac {1}{2}×500a=(1500+250a)$元,乙旅行社的收费为$(a+3)×500×0.8=(1200+400a)$元.
(2)当$a=6$时,$1500+250a=1500+250×6=3000$(元),$1200+400a=1200+400×6=3600$(元).因为$3000<3600$,所以选择甲旅行社较为合算.
(1)解:甲旅行社的收费为$500×3+\frac {1}{2}×500a=(1500+250a)$元,乙旅行社的收费为$(a+3)×500×0.8=(1200+400a)$元.
(2)当$a=6$时,$1500+250a=1500+250×6=3000$(元),$1200+400a=1200+400×6=3600$(元).因为$3000<3600$,所以选择甲旅行社较为合算.
查看更多完整答案,请扫码查看


