《2025年课堂点睛七年级数学上册人教版宁夏专版》

11. 设 $a$ 是最小的自然数,$b$ 是最大的负整数,$c$ 的绝对值为 2,则 $a - b + c = $(C)
A.3
B.$\pm 3$
C.3 或 $-1$
D.1 或 $-3$

答案： C

12. 水利勘察队沿一条河向上游走了 $5.5km$,又继续向上游走了 $4.8km$,然后又向下游走了 $5.2km$,又向下游走了 $4.1km$,这时勘察队在出发点的(A)
A.上游 $1km$ 处
B.下游 $9km$ 处
C.上游 $10.3km$ 处
D.下游 $1km$ 处

答案： A

13. (新考法)按照下图所示的操作步骤,若输入 $x$ 的值为 $-2$,则输出的值为8。
]

答案： 8

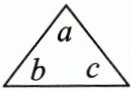
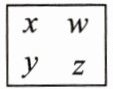
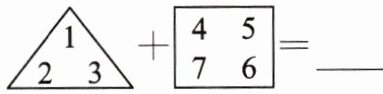
14. (新定义)规定图形$ \begin{array}{c}\triangle \\ \end{array}\begin{array}{c}\triangle \\ $表示运算 a - b + c,图形$ \begin{array}{c}□ \\ \end{array}\begin{array}{c}□ \\ $表示运算 x + z - y - w,则$ \begin{array}{c}\triangle \\ \end{array}\begin{array}{c}\triangle \\ +\begin{array}{c}□ \\ \end{array}\begin{array}{c}□ \\ =$0。

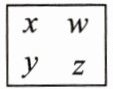
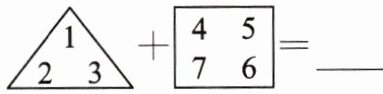
答案： 0

15. 计算：
(1)$-32-(-17)-|-23|+(-15)$；
(2)$-|2\frac{2}{3}-3\frac{1}{3}|-(-2\frac{4}{5})-0.2+|-1\frac{1}{5}|$。

答案：
(1)解：原式=-32+17-23-15=-15-38=-53.
(2)解：原式=$-|-\frac{2}{3}|+2\frac{4}{5}-\frac{1}{5}+1\frac{1}{5}=-\frac{2}{3}+3\frac{4}{5}=\frac{47}{15}$.

16. 已知 $a = -3\frac{1}{4}$,$b = -8\frac{1}{4}$,$c = -2\frac{1}{2}$,求下列各式的值：
(1)$a - b - c$；
(2)$|b|-(a - c)$。

答案：
(1)解：原式=$-3\frac{1}{4}-(-8\frac{1}{4})-(-2\frac{1}{2})=-3\frac{1}{4}+8\frac{1}{4}+2\frac{1}{2}=7\frac{1}{2}$.
(2)原式=$8\frac{1}{4}-(-3\frac{1}{4}+2\frac{1}{2})=8\frac{1}{4}-(-\frac{3}{4})=9$.

17. (核心素养·抽象能力)先观察下列各式,再回答问题。
$\frac{1}{2×3}= \frac{1}{2}-\frac{1}{3}$；$\frac{1}{3×4}= \frac{1}{3}-\frac{1}{4}$；$\frac{1}{4×5}= \frac{1}{4}-\frac{1}{5}$。
(1)①写出：$\frac{1}{5×6}=$$\frac{1}{5}-\frac{1}{6}$；
②请你猜想 $\frac{1}{2022×2024}=$$\frac{1}{2}×(\frac{1}{2022}-\frac{1}{2024})$。
(2)求下列各式的值：
①$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+\frac{1}{4×5}+…+\frac{1}{2024×2025}=$$\frac{2024}{2025}$；
②$\frac{1}{1×3}+\frac{1}{3×5}+\frac{1}{5×7}+\frac{1}{7×9}+…+\frac{1}{2023×2025}=$$\frac{1012}{2025}$。
(3)$\frac{1}{4}+\frac{1}{12}+\frac{1}{24}+\frac{1}{40}+\frac{1}{60}+\frac{1}{84}+\frac{1}{112}+\frac{1}{144}+\frac{1}{180}=$$\frac{9}{20}$。

答案：
(1)①$\frac{1}{5}-\frac{1}{6}$ ②$\frac{1}{2}×(\frac{1}{2022}-\frac{1}{2024})$
(2)①$\frac{2024}{2025}$ ②$\frac{1012}{2025}$
(3)$\frac{9}{20}$