第82页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
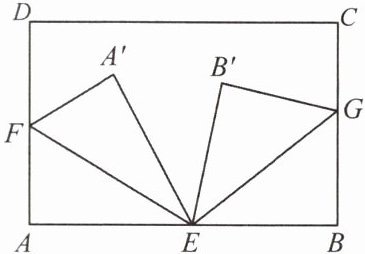
3. 将长方形纸片$ABCD$按下图所示的方式折叠,使$\angle A'EB'= 40^{\circ}$,其中$EF$,$EG$为折痕,则$\angle AEF+\angle BEG$的度数为(
A.$40^{\circ}$
B.$70^{\circ}$
C.$80^{\circ}$
D.$140^{\circ}$
B
)
A.$40^{\circ}$
B.$70^{\circ}$
C.$80^{\circ}$
D.$140^{\circ}$
答案:
B
4. 已知$\angle AOB= 3\angle BOC$,若$\angle BOC= 30^{\circ}$,则$\angle AOC$等于
$60^{\circ}$或$120^{\circ}$
.
答案:
$60^{\circ}$或$120^{\circ}$
5. 【动手操作】
如图,用一副三角尺中的$30^{\circ}和45^{\circ}$这两个角,就可以通过拼接或者叠合的方法画出$75^{\circ}$、$15^{\circ}$的角.
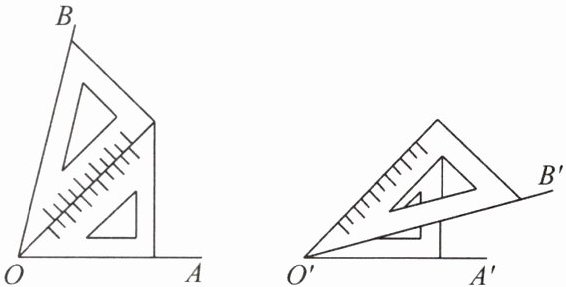
只用$30^{\circ}和45^{\circ}$这两个角,你还可以画出以下哪些度数的角:
①$12^{\circ}$ ②$35^{\circ}$ ③$60^{\circ}$ ④$85^{\circ}$ ⑤$105^{\circ}$ ⑥$135^{\circ}$
【思考表达】
现有$15^{\circ}$、$19^{\circ}$角的两种模板,只能用这两种模板和铅笔画角,小红和小亮各有发现:

利用$12^{\circ}$、$39^{\circ}$角的两种模板,可以画出$3^{\circ}$的角吗?请通过列式计算说明理由.
【类比延伸】
木工师傅有两条长度分别为$30cm和18cm$的笔直木棍,现在木工师傅用这两根木棍可以测出下列哪根木材的长度?
A.$2008cm$
B.$2016cm$
C.$2024cm$
D.$2025cm$
如图,用一副三角尺中的$30^{\circ}和45^{\circ}$这两个角,就可以通过拼接或者叠合的方法画出$75^{\circ}$、$15^{\circ}$的角.

只用$30^{\circ}和45^{\circ}$这两个角,你还可以画出以下哪些度数的角:
③⑤⑥
.(填序号)①$12^{\circ}$ ②$35^{\circ}$ ③$60^{\circ}$ ④$85^{\circ}$ ⑤$105^{\circ}$ ⑥$135^{\circ}$
【思考表达】
现有$15^{\circ}$、$19^{\circ}$角的两种模板,只能用这两种模板和铅笔画角,小红和小亮各有发现:

利用$12^{\circ}$、$39^{\circ}$角的两种模板,可以画出$3^{\circ}$的角吗?请通过列式计算说明理由.
可以,39 - 3×12 = 3
【类比延伸】
木工师傅有两条长度分别为$30cm和18cm$的笔直木棍,现在木工师傅用这两根木棍可以测出下列哪根木材的长度?
B
.A.$2008cm$
B.$2016cm$
C.$2024cm$
D.$2025cm$
答案:
③⑤⑥;可以,39 - 3×12 = 3;B
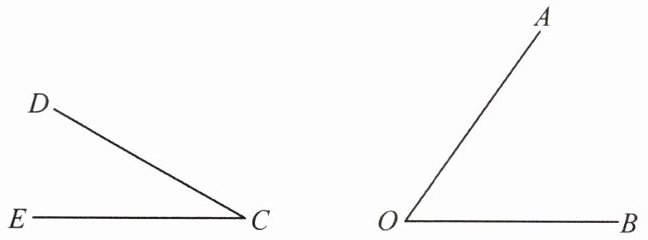
6. 如图,已知$\angle DCE$,$\angle AOB$,利用尺规作图比较它们的大小(不写作法,保留作图痕迹).

答案:
解:以$O$为顶点,$OB$为一边作$\angle BOF = \angle DCE$,若$\angle AOB$与$\angle BOF$重合,则$\angle AOB=\angle DCE$;若$\angle AOB$在$\angle BOF$内部,则$\angle AOB\lt\angle DCE$;若$\angle AOB$在$\angle BOF$外部,则$\angle AOB\gt\angle DCE$(作图痕迹略)。
如图甲所示,将一副三角尺的直角顶点重合在点$O$处.
 (1) ①$\angle AOD和\angle BOC$相等吗?说明理由;
(1) ①$\angle AOD和\angle BOC$相等吗?说明理由;
②$\angle AOC和\angle BOD$在数量上有何关系?说明理由.
(2) 若将这副三角尺按图乙所示方式摆放,三角尺的直角顶点重合在点$O$处.
①$\angle AOD和\angle BOC$相等吗?说明理由;
②$\angle AOC和\angle BOD$的以上关系还成立吗?说明理由.
 (1) ①$\angle AOD和\angle BOC$相等吗?说明理由;
(1) ①$\angle AOD和\angle BOC$相等吗?说明理由;②$\angle AOC和\angle BOD$在数量上有何关系?说明理由.
(2) 若将这副三角尺按图乙所示方式摆放,三角尺的直角顶点重合在点$O$处.
①$\angle AOD和\angle BOC$相等吗?说明理由;
②$\angle AOC和\angle BOD$的以上关系还成立吗?说明理由.
答案:
(1)①相等.理由:
∵∠AOB=90°,∠COD=90°,
∴∠AOB+∠BOD=∠COD+∠BOD,即∠AOD=∠BOC.
②∠AOC+∠BOD=180°.理由:
∵∠AOC=∠AOB+∠BOC=90°+∠BOC,∠BOD=∠COD-∠BOC=90°-∠BOC,
∴∠AOC+∠BOD=90°+∠BOC+90°-∠BOC=180°.
(2)①相等.理由:
∵∠AOB=90°,∠COD=90°,
∴∠AOB-∠AOC=∠COD-∠AOC,即∠BOC=∠AOD.
②成立,∠AOC+∠BOD=180°.理由:
∵∠AOC=∠AOB-∠BOC=90°-∠BOC,∠BOD=∠COD+∠BOC=90°+∠BOC,
∴∠AOC+∠BOD=90°-∠BOC+90°+∠BOC=180°.
(1)①相等.理由:
∵∠AOB=90°,∠COD=90°,
∴∠AOB+∠BOD=∠COD+∠BOD,即∠AOD=∠BOC.
②∠AOC+∠BOD=180°.理由:
∵∠AOC=∠AOB+∠BOC=90°+∠BOC,∠BOD=∠COD-∠BOC=90°-∠BOC,
∴∠AOC+∠BOD=90°+∠BOC+90°-∠BOC=180°.
(2)①相等.理由:
∵∠AOB=90°,∠COD=90°,
∴∠AOB-∠AOC=∠COD-∠AOC,即∠BOC=∠AOD.
②成立,∠AOC+∠BOD=180°.理由:
∵∠AOC=∠AOB-∠BOC=90°-∠BOC,∠BOD=∠COD+∠BOC=90°+∠BOC,
∴∠AOC+∠BOD=90°-∠BOC+90°+∠BOC=180°.
查看更多完整答案,请扫码查看


