《2025年精练课堂分层作业七年级数学上册北师大版》

1. 观察一列数的特点：0,1,-4,9,-16,25,…,则第11个数是(B)
A.-121
B.-100
C.100
D.121

答案： B

2. 观察一串数：0,2,4,6,…,则第n个数是(A)
A.2(n - 1)
B.2n - 1
C.2(n + 1)
D.2n + 1

答案： A

1. 一组数列：2,5,10,17,26,…,依此类推,第n个数是(A)
$A. n^2 + 1$
$B. n^2 - 1$
$C. n^2 + 2$
$D. n^2 - 2$

答案： A

2. (2023·黑龙江牡丹江中考)观察下面两行数：
1,5,11,19,29,…；
1,3,6,10,15,…
取每行数的第7个数,计算这两个数的和是(C)
A.92
B.87
C.83
D.78

答案： C

3. 下表中的数字是按一定规律填写的,表中a的值应是21.

答案： 21

4. (2023·湖南岳阳中考)观察下列式子：
$1^2 - 1 = 1×0；$$2^2 - 2 = 2×1；$$3^2 - 3 = 3×2；$$4^2 - 4 = 4×3；$$5^2 - 5 = 5×4；$…
依此规律,第n(n为正整数)个等式是$n^2 - n = n(n - 1)$.

答案： $n^2 - n = n(n - 1)$

5. 黑洞是一种引力极大的天体,连光都逃脱不了它的束缚.数学中也存在着神奇的“黑洞数”现象：

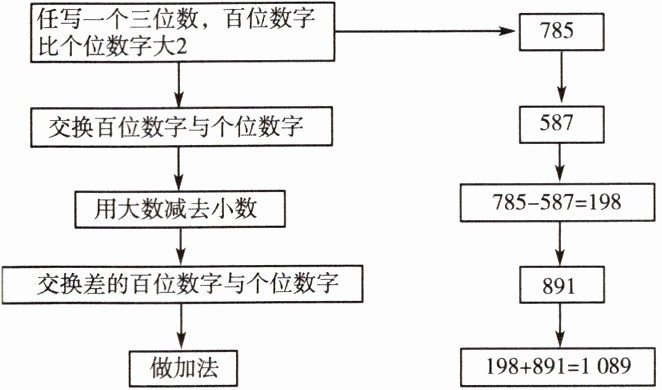
(1)请你用不同的三个数再试试,你发现了什么“神奇”的现象？
(2)请用学过的知识解释(1)中的发现.

答案：
(1)示例1：取三位数321（百位3，个位1，3-1=2）。交换百位与个位得123，321-123=198，交换198得891，198+891=1089。
示例2：取三位数543（百位5，个位3，5-3=2）。交换百位与个位得345，543-345=198，交换198得891，198+891=1089。
发现：无论选取哪个百位数字比个位数字大2的三位数，按上述步骤操作后，结果均为1089。
(2)设三位数的百位数字为a，十位数字为b，个位数字为c，且a=c+2（a，c为1-9的整数，b为0-9的整数）。
原数表示为100a+10b+c，交换百位与个位后为100c+10b+a。
大数减小数：(100a+10b+c)-(100c+10b+a)=99(a-c)=99×2=198。
交换198的百位与个位得891，198+891=1089。
故结果恒为1089。

6. 观察下列有规律的数：$\frac{1}{2}$,$\frac{1}{6}$,$\frac{1}{12}$,$\frac{1}{20}$,$\frac{1}{30}$,$\frac{1}{42}$,…,根据规律可知：
(1)第7个数是$\frac{1}{56}$,第n个数是$\frac{1}{n(n + 1)}$(n为正整数)；
(2)$\frac{1}{132}$是第11个数；
(3)计算$\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}+…+\frac{1}{2022×2023}$的值.
$\frac{2022}{2023}$

答案：
(1)
第7个数：观察数列$\frac{1}{2}$，$\frac{1}{6}$，$\frac{1}{12}$，$\frac{1}{20}$，$\frac{1}{30}$，$\frac{1}{42}\ldots$，
可以发现分母是连续自然数的乘积，$1× 2$，$2× 3$，$3× 4$，$4× 5$，$5× 6$，$6× 7\ldots$，
所以第7个数，分母是$7× 8 = 56$，该数是$\frac{1}{56}$；
第$n$个数：根据上述规律，第$n$个数的分母为$n(n + 1)$，所以第$n$个数是$\frac{1}{n(n + 1)}$。
(2)
因为分母为$n(n + 1)=132$，即$n^{2}+n - 132=0$，
因式分解得$(n - 11)(n+12)=0$，
解得$n = 11$或$n=-12$（舍去），
所以$\frac{1}{132}$是第$11$个数。
(3)
$\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}+\cdots+\frac{1}{2022×2023}$
$=\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+\frac{1}{4×5}+\frac{1}{5×6}+\cdots+\frac{1}{2022×2023}$
$=(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+(\frac{1}{4}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{6})+\cdots+(\frac{1}{2022}-\frac{1}{2023})$
$=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\cdots+\frac{1}{2022}-\frac{1}{2023}$
$=1-\frac{1}{2023}$
$=\frac{2022}{2023}$
综上，答案依次为：
(1)$\frac{1}{56}$；$\frac{1}{n(n + 1)}$；
(2)$11$；
(3)$\frac{2022}{2023}$。