《2025年精练课堂分层作业七年级数学上册北师大版》

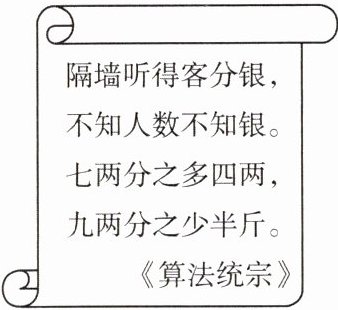
1. 下图是明代数学家程大位的《算法统宗》中的一个问题,其大意为：有一群人分银子,如果每人分七两,则剩余四两；如果每人分九两,则还差八两(注：明代时1斤= 16两,故有“半斤八两”这个成语,设未知数列方程正确顺序的序号是______.

①设这群人人数为x,根据题意得$7x - 4 = 9x + 8$；
②设这群人人数为x,根据题意得$7x + 4 = 9x - 8$；
③设所分银子的数量为x两,根据题意得$\frac{x - 4}{7} = \frac{x + 8}{9}$；
④设所分银子的数量为x两,根据题意得$\frac{x - 4}{7} = \frac{x - 8}{9}$
②③

答案： ②③

2. 洛书(如图①),古称龟书,现已入选国家级非物质文化遗产名录.洛书是术数中乘法的起源,“戴九履一,左三右七,二四为肩,六八为足,五居中宫”是对洛书形象的描述,洛书对应的九宫格(如图②)填有1到9这九个正整数,满足任意一行、列、对角线上三个数之和相等.洛书的填法古人是怎么找到的呢？在学习了方程相关知识后,小凯尝试探究其中的奥秘.

(1)【第一步】设任意一行、列、对角线上三个数之和为S,则每一行三个数的和均为S,而这9个数的和恰好为1到9这9个正整数之和,由此可得S= 15；
(2)【第二步】再设中间数为x,利用包含中间数x的行、列、对角线上的数与9个数的关系可列出方程,求解中间数x.
请你根据上述探究,列方程求出中间数x的值.
因为九宫格中所有数之和为45，且每行、每列、两条对角线的和均为15，中间数x在行、列、两条对角线中各被计算一次，共参与4次求和，所以可列方程：45 + 3x = 4×15，即45 + 3x = 60，移项得3x = 15，解得x = 5。

答案： （1）$1$到$9$的和为$1 + 2 + 3 + \cdots + 9 = 45$，因为九宫格有三行，且每行和为$S$，所以$3S = 45$，解得$S = 15$。
故本题答案为$15$。
（2）以中间数$x$为中心，根据洛书数字排列规律可得方程：
$1 + 2 + \cdots+ 9 + 4x = 3× 15$（$4x$为中间数在行、列及两条对角线中重复计算的值），
即$45 + 3x = 45$（该步骤（2）中方程列式思路错误，下面为正确思路）
根据洛书数字排列规律，中间数参与$1$次行、$1$次列、$2$次对角线和的计算，所以可列方程：
$1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9+3x = 3× 15× 3 - 3x$（此思路复杂且错误），
正确思路为：因为九宫格中所有数之和为$45$，且每行（列、对角线）和为$15$，中间数$x$在行、列、两条对角线中都被计算了一次，所以可列方程$45 + 3x = 3× 15× 2 - 3x$（复杂错误），
最简单思路：由于九宫格中所有数之和为$45$，且每行（列、对角线）和为$15$，中间数$x$参与了$1$行、$1$列、$2$条对角线的和的计算，所以$45+3x = 4× 15$，
即$45 + 3x = 60$，
移项可得$3x = 60 - 45$，
即$3x = 15$，
解得$x = 5$。
故中间数$x$的值为$5$。