《2025年精练课堂分层作业七年级数学上册北师大版》

7.若单项式$\frac{1}{2}xy^{2m - 1}$与单项式$- 5^{2}x^{2}y^{2}$的次数相同,则$m = $2.

答案： 2

8.若关于$x$,$y的多项式x^{2} - 2x^{2}y + ●y^{2}的各项系数之和是5$,则“$●$”代表的数是6.

答案： 6

9.已知多项式$2x^{5} + (m + 1)x^{4} + 3x - (n - 2)x^{2} + 3不含x$的偶次方,求出$2m + n$的值.

答案： 由题意，多项式$2x^{5} + (m + 1)x^{4} + 3x - (n - 2)x^{2} + 3$不含$x$的偶次方项，
所以，含$x$的偶次方的项的系数必须为0，
即$m + 1 = 0$和$-(n - 2) = 0$，
解得$m = -1$，$n = 2$，
所以，$2m + n = 2×(-1) + 2 = 0$，
所以$2m + n$的值为$0$。

10.如果$\vert a + 1\vert + (b - 2)^{2} = 0$,那么单项式$- x^{a + b}y^{b - a}$的次数是多少?

答案： 由题意，$\vert a + 1\vert + (b - 2)^{2} = 0$，
因为$\vert a + 1\vert$和$(b - 2)^{2}$都是非负数，且它们的和为0，
所以$\vert a + 1\vert = 0$，$(b - 2)^{2} = 0$，
解得$a = - 1$，$b = 2$，
将$a$和$b$的值代入单项式$- x^{a + b}y^{b - a}$，
得到$- x^{-1 + 2}y^{2 - (-1)} = - x y^{3}$，
单项式的次数为$1 + 3 = 4$。
答：单项式$- x^{a + b}y^{b - a}$的次数是$4$。

11.如图,某长方形广场的四个角都有一块半径相同的四分之一圆形的草地.圆形的半径为$r$米,长方形的长为$a$米,宽为$b$米.

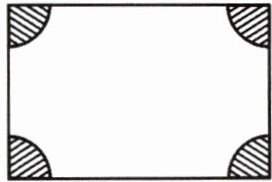
(1)分别用代数式表示草地和空地的面积；
(2)若长方形的长为$300$米,宽为$200$米,圆形的半径为$10$米,求广场空地的面积.(计算结果保留到整数)

答案：
(1)四块四分之一圆形合起来是一个整圆，
草地面积：$\pi r^{2}$（平方米），
长方形广场面积：$ab$（平方米），
空地面积：$(ab - \pi r^{2})$（平方米）。
(2)把$a = 300$，$b = 200$，$r = 10$代入$ab - \pi r^{2}$得：
$300×200 - \pi×10^{2}$
$= 60000 - 100\pi$
$\approx 60000 - 100×3.1416$
$\approx 60000 - 314.16$
$\approx 59686$（平方米）
答：广场空地的面积约为$59686$平方米。

12.试写出同时满足下列条件的多项式：
①该多项式中只含字母$a$；
②该多项式中常数项的倒数等于它本身；
③该多项式的次数是$2$；
④该多项式中各单项式(常数除外)的系数均为$- 3$.

答案： 1. $-3a^{2}-3a+1$
2. $-3a^{2}-3a-1$
3. $-3a^{2}+1$
4. $-3a^{2}-1$

观察下列一串单项式：
$xy$,$- 2x^{2}y$,$4x^{3}y$,$- 8x^{4}y$,$16x^{5}y$,…$$.
(1)按此规律写出第$9$个单项式；
(2)第$n$个单项式是什么?它的系数和次数分别是多少?

答案：
(1)
前几个单项式的系数分别为$1 =(-1)^{1 + 1}×2^{0}$，$-2=(-1)^{2 + 1}×2^{1}$，$4 =(-1)^{3+1}×2^{2}$，$-8=(-1)^{4 + 1}×2^{3}$，$16=(-1)^{5+1}×2^{4}$；
$x$的次数与单项式的序号数相同，$y$的次数始终为$1$。
第$9$个单项式，序号$n = 9$，系数为$(-1)^{9+1}×2^{8}=256$，$x$的次数为$9$，$y$的次数为$1$，所以第$9$个单项式为$256x^{9}y$。
(2)
第$n$个单项式，系数为$(-1)^{n + 1}×2^{n-1}$，$x$的次数为$n$，$y$的次数为$1$，所以第$n$个单项式是$(-1)^{n + 1}×2^{n-1}x^{n}y$。
系数为$(-1)^{n + 1}×2^{n-1}$，次数为$n + 1$。