《2025年精练课堂分层作业七年级数学上册北师大版》

5. 判断正误.
(1) 用一个平面去截一个正方体, 截出的面一定是正方形或长方形. (错)
(2) 用一个平面去截一个圆柱, 截出的面一定是圆. (错)
(3) 用一个平面去截圆锥, 截出的面一定是三角形. (错)
(4) 用一个平面去截一个球, 无论如何截, 截面都是一个圆. (对)

答案：
(1)错
(2)错
(3)错
(4)对

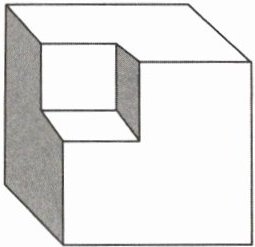
6. 下图是棱长为 $2 cm$ 的正方体, 过相邻三条棱的中点截取一个小正方体, 则剩下部分的表面积为 $24 cm^2$.

答案： 24

7. 指出下列几何体的截面形状.
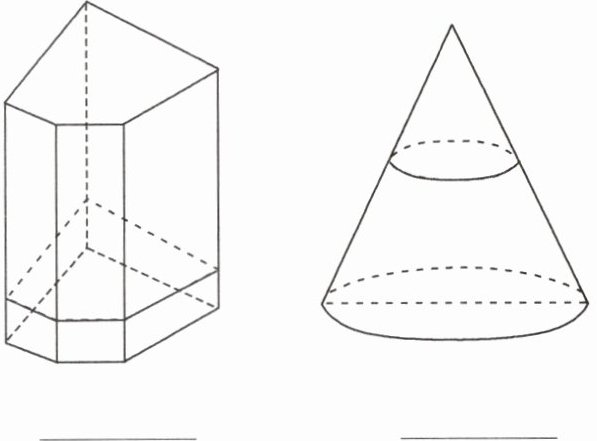
六边形圆形

答案： 六边形 圆形

8. 用一个平面截一个圆锥, 所得截面可能是三角形吗? 可能是直角三角形吗? 当截面是一个圆时, 截面面积可能恰好等于底面面积的一半吗?

答案： 1. 可能是三角形。当平面经过圆锥的顶点且与底面相交时，截面为三角形。
2. 可能是直角三角形。当圆锥的高等于底面半径时，过顶点且垂直于底面的平面（轴截面）截得的等腰三角形为直角三角形（腰长²+腰长²=底边²，即2(h²+r²)=(2r)²，h=r时成立）。
3. 可能。当截面平行于底面时为圆，设底面半径为r，截面半径为r'，由相似三角形得r'/r=h'/h（h'为截面到顶点距离，h为圆锥高）。截面面积为底面一半时，πr'²=(1/2)πr²，r'=r/√2，此时h'=h/√2（h'＜h，存在），故可能。

9. 一个正方体容器, 内有一定体积的水, 上面浮着一层黄色的油, 如果将容器朝不同方向倾斜, 便可观察到类似于截面的现象. 试一试, 你看到了哪几种形状的截面?

答案： 答题区域：
当正方体容器朝不同方向倾斜时，可观察到以下形状的截面：
三角形、四边形（包括矩形、平行四边形、梯形）、五边形、六边形。

10. 用一个平面去截一个几何体, 如果截面的形状是正方形, 你能想象出这个几何体原来的形状吗?

答案： 1. 正方体：平面平行于正方体的任意一个面去截，截面为正方形。
2. 长方体：当长方体有两个相对的面是正方形时，平面平行于这两个面去截，截面为正方形；或长方体的长、宽、高中有两个相等，平面平行于对应面去截，截面为正方形。
3. 圆柱体：当圆柱体的底面直径等于高时，平面垂直于底面且经过底面直径去截，截面为正方形。

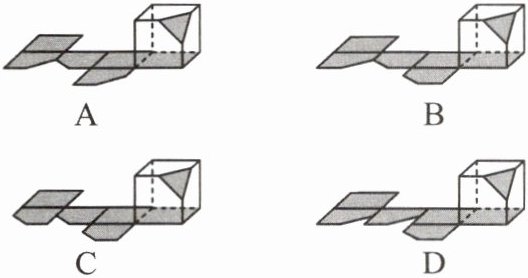
过正方体中有公共顶点的三条棱的中点切出一个面, 得到右图所示的几何体. 该几何体展开图为 (B)

答案： B