第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
4.若$∠A= 20^{\circ }18',∠B= 20^{\circ }15'30'',∠C= 20.25^{\circ }$,则下列判断正确的是 (
A.$∠A>∠B>∠C$
B.$∠B>∠A>∠C$
C.$∠A>∠C>∠B$
D.$∠C>∠A>∠B$
A
)A.$∠A>∠B>∠C$
B.$∠B>∠A>∠C$
C.$∠A>∠C>∠B$
D.$∠C>∠A>∠B$
答案:
A
5.如图,OC是表示北偏西$63^{\circ }17'$方向的一条射线,则$∠BOC$的度数是 (
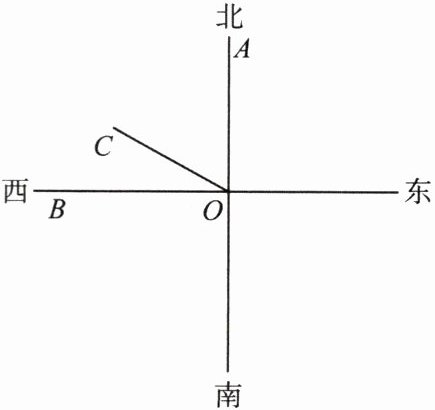
A.$26^{\circ }34'$
B.$26^{\circ }43'$
C.$27^{\circ }43'$
D.$27^{\circ }53'$
B
)
A.$26^{\circ }34'$
B.$26^{\circ }43'$
C.$27^{\circ }43'$
D.$27^{\circ }53'$
答案:
B
6.当钟上显示1点30分时,时针与分针所成夹角的度数为 (
A.$130^{\circ }$
B.$135^{\circ }$
C.$150^{\circ }$
D.$210^{\circ }$
B
)A.$130^{\circ }$
B.$135^{\circ }$
C.$150^{\circ }$
D.$210^{\circ }$
答案:
B
7.如图,用一副三角板可以画出$15^{\circ }$的角,用它们还可以画出其他一些特殊角.不能利用这副三角板直接画出的角度是 (
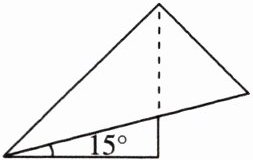
A.$55^{\circ }$
B.$75^{\circ }$
C.$105^{\circ }$
D.$135^{\circ }$
A
)
A.$55^{\circ }$
B.$75^{\circ }$
C.$105^{\circ }$
D.$135^{\circ }$
答案:
A
8.$\frac {1}{2}$平角=
1
直角,$\frac {1}{4}$周角=$\frac{1}{2}$
平角=1
直角,$135^{\circ }$角=$\frac{3}{4}$
平角.
答案:
1;$\frac{1}{2}$;1;$\frac{3}{4}$
9.计算:$24^{\circ }24'=$
24.4
$^{\circ }$.
答案:
$24.4$
10.(1)钟上分针每转动一周,时针转动
(2)秒针每转动一周,分针转动
30
度; (2)秒针每转动一周,分针转动
6
度,时针转动0.5
度.
答案:
(1)30;
(2)6,0.5
(1)30;
(2)6,0.5
11.如图,点O表示小明家,A,B,C,D,E分别表示学校、高铁站、博物馆、影院、公园,且$2OB= 3OC= 6OA= 6km$,E是OC的中点,$BD= 2OD$.
(1)判断到点O的距离相等的地方有哪些?
(2)以小明家为参照点,请用方位角和实际距离分别表示学校、公园、博物馆、影院、高铁站的位置.
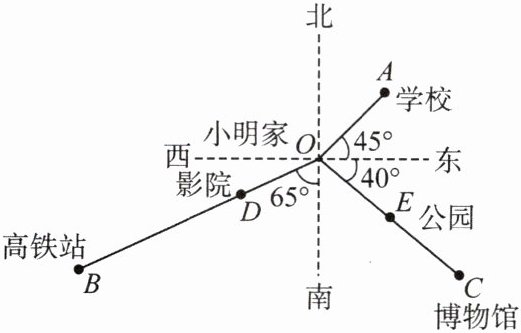
(1)判断到点O的距离相等的地方有哪些?
(2)以小明家为参照点,请用方位角和实际距离分别表示学校、公园、博物馆、影院、高铁站的位置.

答案:
(1) 由题意得:$6OA=6km$,则$OA=1km$;$2OB=6km$,则$OB=3km$;$3OC=6km$,则$OC=2km$。
$E$是$OC$中点,故$OE=\frac{1}{2}OC=1km$。
设$OD=x$,由$BD=2OD$得$BD=2x$,又$OB=OD+BD=x+2x=3x=3km$,解得$OD=1km$。
综上,$OA=OD=OE=1km$,即学校(A)、影院(D)、公园(E)到点O的距离相等。
(2) 学校(A):东偏北$45°$方向,$1km$;
公园(E):东偏南$40°$方向,$1km$;
博物馆(C):东偏南$40°$方向,$2km$;
影院(D):西偏南$65°$方向,$1km$;
高铁站(B):西偏南$65°$方向,$3km$。
(1) 由题意得:$6OA=6km$,则$OA=1km$;$2OB=6km$,则$OB=3km$;$3OC=6km$,则$OC=2km$。
$E$是$OC$中点,故$OE=\frac{1}{2}OC=1km$。
设$OD=x$,由$BD=2OD$得$BD=2x$,又$OB=OD+BD=x+2x=3x=3km$,解得$OD=1km$。
综上,$OA=OD=OE=1km$,即学校(A)、影院(D)、公园(E)到点O的距离相等。
(2) 学校(A):东偏北$45°$方向,$1km$;
公园(E):东偏南$40°$方向,$1km$;
博物馆(C):东偏南$40°$方向,$2km$;
影院(D):西偏南$65°$方向,$1km$;
高铁站(B):西偏南$65°$方向,$3km$。
如图,在锐角$∠AOB$内部画1条射线,可得
]
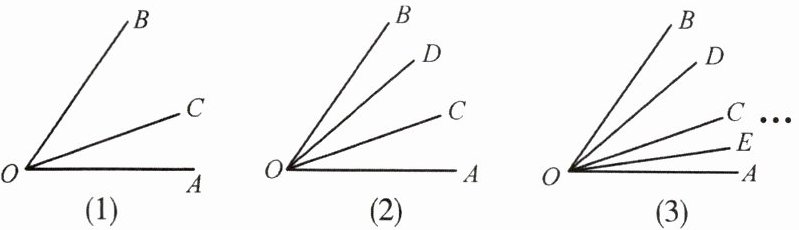
3
个锐角;画2条不同射线,可得____6
个锐角;画3条不同射线,可得____10
个锐角……照此规律,画n条不同射线,可得____$\frac{(n+1)(n+2)}{2}$
个锐角.]

答案:
3;6;10;$\frac{(n+1)(n+2)}{2}$
查看更多完整答案,请扫码查看


