《2025年精练课堂分层作业七年级数学上册北师大版》

1.将一个正方体的表面沿某些棱剪开,能展开成下列平面图形吗？
(1) (2) (3)

答案：
(1)能
(2)不能
(3)能

2.仔细观察,想一想在下图中,哪些图是正方体的表面展开图？
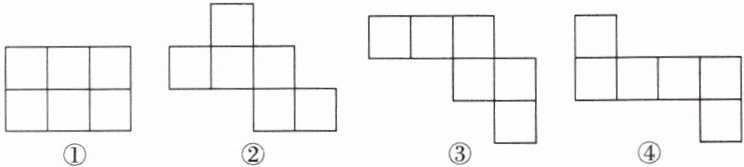
① ② ③ ④

答案： 答题卡：
根据正方体表面展开图的特征，①属于“田”字格，不是正方体表面展开图；②属于“1 - 4 - 1”型，是正方体表面展开图；③不是正方体表面展开图；④属于“1 - 4 - 1”型，是正方体表面展开图。
综上，②④是正方体的表面展开图。

3.在无阴影的方格中再画上2个阴影方格,使它们与图中4个有阴影的方格可以构成一个正方体的表面展开图.

答案： 1. 对于图①：
正方体表面展开图的形式有“$1 - 4 - 1$”型、“$2 - 3 - 1$”型、“$2 - 2 - 2$”型、“$3 - 3$”型等。
图①中已有$4$个阴影方格呈“一”字排列（类似“$1 - 4 - 1$”型的中间$4$个），我们可以在两端添加阴影方格。
例如，在最左边一列的上下两个方格（或最右边一列的上下两个方格）画上阴影方格。
2. 对于图②：
图②中已有阴影方格的分布，我们可以根据“$2 - 3 - 1$”型来添加。
可以在第一行最左边方格和第三行最右边方格（或第一行最右边方格和第三行最左边方格）画上阴影方格。
所以，图①可在两端（如最左列上下格或最右列上下格）添加阴影方格；图②可按“$2 - 3 - 1$”型（如第一行最左和第三行最右或第一行最右和第三行最左）添加阴影方格（答案不唯一）。

4.如图①,点A,B是正方体上的两个顶点,将正方体按图②所示方式展开,则在展开图中点B的位置是哪个点呢？
图① 图②

答案： 本题可通过分析正方体展开图的特征，确定点$B$在展开图中的位置。
在正方体中，点$A$、$B$是相邻顶点，在展开图中，相邻顶点在展开后应处于相邻的位置。
观察图②的展开图，与点$A$相邻且符合正方体展开关系的点为$B_{2}$。
所以在展开图中点$B$的位置是点$B_{2}$。

5.马小虎准备制作一个封闭的正方体盒子,他先用4个大小一样的正方形制成下图中的拼接图形(实线部分),经折叠后发现还少一个面.请你在下图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(添加所有符合要求的正方形,添加的正方形用阴影表示)

答案： 答题卡：
新拼接图形如下（阴影部分为添加的正方形）：
情况一：在第一幅图右侧中间小正方形右侧添加一个正方形。
| | | | | |
| --- | --- | --- | --- | --- |
| | | | | |
| |□|□|□| |
| |□| |□| |
| | |□| | |
| | | | | |
情况二：在第二幅图上侧中间小正方形上侧添加一个正方形。
| | |□| | |
| --- | --- | --- | --- | --- |
| | |□| | |
| | |□| | |
| |□|□|□| |
| | | | | |
情况三：在第三幅图下侧中间小正方形下侧添加一个正方形。
| | | | | |
| --- | --- | --- | --- | --- |
| | |□| | |
| | |□| | |
| | |□| | |
| |□|□|□| |
情况四：在第四幅图左侧中间小正方形左侧添加一个正方形。
| | | | | |
| --- | --- | --- | --- | --- |
| | | | | |
|□|□|□| | |
|□| |□| | |
|□| | | | |
结论：共有4种添加方式。

6.将下图的正方体沿图中粗黑的棱剪开,把它展开成平面图形,则图中的线段AB与CD在展开图中,它们所在的直线之间的位置关系是什么呢？

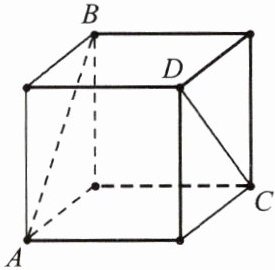
答案： 沿粗黑棱剪开展开成平面图形（展开图不唯一），通过分析正方体展开图中线段AB与CD的位置，在原正方体中AB与CD是异面垂直的棱，展开后变为在同一平面，根据正方体棱的关系可知它们所在的直线是平行关系。
所以线段AB与CD在展开图中所在的直线之间的位置关系是平行。

7.如图所示,在边长为4的正方形中包含16个一样的边长为1的小正方形.有两个图中已经将6个小正方形涂黑,恰好是正方体的平面展开图.开动脑筋,你还能在空白图中画出不同的正方体展开方式吗？

答案： 本题可根据正方体展开图的特征来画出不同的展开方式。
正方体展开图有$11$种基本形式，包括“$1 - 4 - 1$”型、“$2 - 3 - 1$”型、“$2 - 2 - 2$”型、“$3 - 3$”型。已知已有两种展开方式，我们可以按照“$1 - 4 - 1$”型、“$2 - 3 - 1$”型等形式进行绘制（答案不唯一）。
以下为一种可能的绘制方式（涂黑部分表示正方体展开图）：
第一行从左到右第三个图：
第一行第二列、第二行第一列、第二行第二列、第二行第三列、第三行第二列、第四行第二列小正方形涂黑。
第二行从左到右第一个图：
第一行第三列、第二行第一列、第二行第二列、第二行第三列、第三行第二列、第四行第三列小正方形涂黑。
（你可以根据正方体展开图的特征画出其他多种不同的展开方式）