第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
13. 将长方形 $ ABCD $ 沿 $ AE $ 折叠,得到的图形如图所示。若 $ \angle CED' = 56^{\circ} $,则 $ \angle AED $ 的大小是
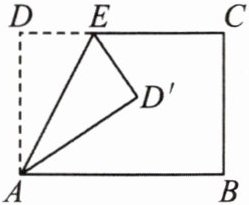
62°
。
答案:
62°
14. 如图,已知 $ \angle AOC = \angle BOD = 90^{\circ} $,$ \angle AOD = 150^{\circ} $,则 $ \angle BOC $ 的度数为(
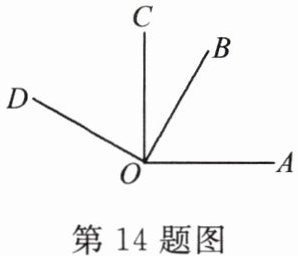
A.$ 30^{\circ} $
B.$ 45^{\circ} $
C.$ 50^{\circ} $
D.$ 60^{\circ} $
A
)
A.$ 30^{\circ} $
B.$ 45^{\circ} $
C.$ 50^{\circ} $
D.$ 60^{\circ} $
答案:
A
15. 如图,若 $ \angle AOB = \angle COD $,则(
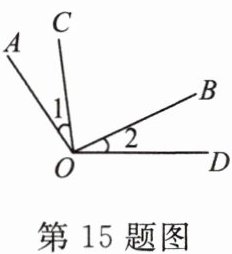
A.$ \angle 1 > \angle 2 $
B.$ \angle 1 < \angle 2 $
C.$ \angle 1 = \angle 2 $
D.$ \angle 1 $,$ \angle 2 $ 的大小关系不确定
C
)
A.$ \angle 1 > \angle 2 $
B.$ \angle 1 < \angle 2 $
C.$ \angle 1 = \angle 2 $
D.$ \angle 1 $,$ \angle 2 $ 的大小关系不确定
答案:
C
16. 如图,在 $ \triangle ABC $ 中,$ \angle BAC = 90^{\circ} $,将 $ Rt \triangle ABC $ 绕点 $ A $ 逆时针旋转 $ \alpha $ 度($ 0^{\circ} < \alpha < 90^{\circ} $),得到 $ \triangle DAE $,则 $ \angle BAE + \angle DAC $ 的度数为(
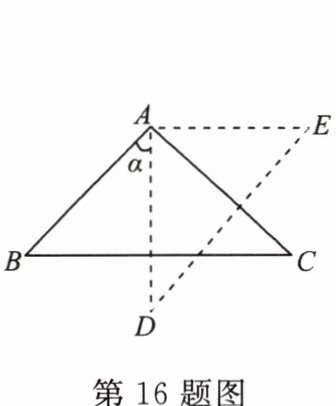
A.$ 90^{\circ} + 2\alpha $
B.$ 180^{\circ} + \alpha $
C.$ 180^{\circ} - \alpha $
D.$ 180^{\circ} $
D
)
A.$ 90^{\circ} + 2\alpha $
B.$ 180^{\circ} + \alpha $
C.$ 180^{\circ} - \alpha $
D.$ 180^{\circ} $
答案:
D
17. 一个正方形和两个等边三角形的位置如图所示,若 $ \angle 3 = 50^{\circ} $,则 $ \angle 1 + \angle 2 = $(
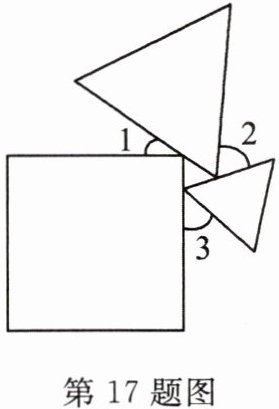
A.$ 90^{\circ} $
B.$ 100^{\circ} $
C.$ 130^{\circ} $
D.$ 180^{\circ} $
B
)
A.$ 90^{\circ} $
B.$ 100^{\circ} $
C.$ 130^{\circ} $
D.$ 180^{\circ} $
答案:
B
18. 把一副三角板按下图所示的方式拼在一起,则 $ \angle ABC $ 的大小为(
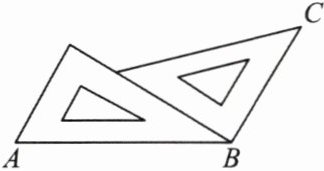
A.$ 90^{\circ} $
B.$ 100^{\circ} $
C.$ 120^{\circ} $
D.$ 135^{\circ} $
C
)
A.$ 90^{\circ} $
B.$ 100^{\circ} $
C.$ 120^{\circ} $
D.$ 135^{\circ} $
答案:
C
19. 一个角的补角加上 $ 10^{\circ} $ 后,等于这个角的余角的 $ 3 $ 倍,则这个角是(
A.$ 30^{\circ} $
B.$ 35^{\circ} $
C.$ 40^{\circ} $
D.$ 45^{\circ} $
C
)A.$ 30^{\circ} $
B.$ 35^{\circ} $
C.$ 40^{\circ} $
D.$ 45^{\circ} $
答案:
C
20. 如图,$ \angle AOB = 72^{\circ}32' $,射线 $ OC $ 在 $ \angle AOB $ 内,$ \angle BOC = 30^{\circ}40' $,则 $ \angle AOC = $
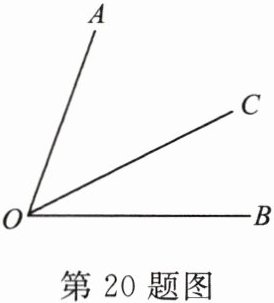
$41^{\circ}52'$
。
答案:
$41^{\circ}52'$
21. 如图,将三个相同正方形的一个顶点重合放置,且 $ \angle COE = 40^{\circ} $,$ \angle BOF = 30^{\circ} $,则 $ \angle AOD = $
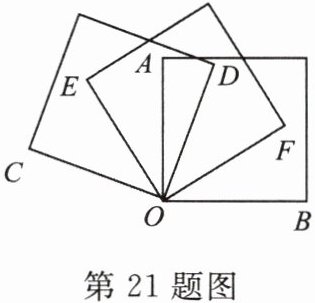
20
$ ^{\circ} $。
答案:
20
22. 如图,已知 $ \angle AOB $,以 $ OA $ 为边作 $ \angle AOC $,使 $ \angle BOC = \frac{1}{2} \angle AOB $,则下列结论成立的是(
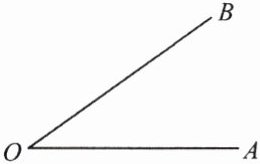
A.$ \angle AOC = \angle BOC $
B.$ \angle AOC < \angle AOB $
C.$ \angle AOC = \angle BOC $ 或 $ \angle AOC = 2 \angle BOC $
D.$ \angle AOC = \angle BOC $ 或 $ \angle AOC = 3 \angle BOC $
D
)
A.$ \angle AOC = \angle BOC $
B.$ \angle AOC < \angle AOB $
C.$ \angle AOC = \angle BOC $ 或 $ \angle AOC = 2 \angle BOC $
D.$ \angle AOC = \angle BOC $ 或 $ \angle AOC = 3 \angle BOC $
答案:
D
23. 以 $ \angle AOB $ 的顶点 $ O $ 为端点引射线 $ OC $,使 $ \angle AOC : \angle BOC = 5 : 4 $,若 $ \angle AOB = 27^{\circ} $,则 $ \angle AOC = $
15°或135°
。
答案:
15°或135°
24. $ OC $ 是从 $ \angle AOB $ 的顶点 $ O $ 引出的一条射线,若 $ \angle AOB = 90^{\circ} $,$ \angle AOB = 2 \angle BOC $,则 $ \angle AOC $ 的度数是
45°或135°
。
答案:
45°或135°
查看更多完整答案,请扫码查看


