《2025年精练课堂分层作业七年级数学上册北师大版》

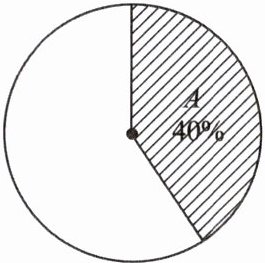
5. 下图是地球表面积统计图的一部分,扇形 $ A $ 表示地球某几种水域的面积,则此扇形的圆心角为144度.
]

答案： 144

6. 对正方形剪一刀能得到三、四或五边形.

答案： 三、四或五

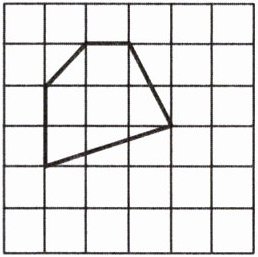
7. 各顶点都在方格纸的格点(横竖格子线的交点)上的多边形称为格点多边形,它的面积 $ S $ 可用公式 $ S = a + \frac{1}{2} b - 1 $ ($ a $ 是多边形内的格点数,$ b $ 是多边形边界上的格点数)计算,这个公式被称为“皮克定理”.下图给出了一个格点五边形,则该五边形的面积 $ S = $6.
]

答案： 6

8. 如图,方格纸中 $ 4 $ 个小正方形的边长均为 $ 1 $,则图中阴影部分三个小扇形的面积和为$\frac{\pi}{2}$.(结果保留 $ \pi $)
]

答案： $\frac{\pi}{2}$

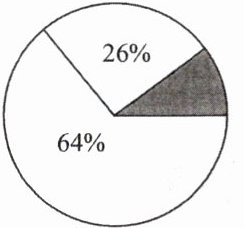
9. 如图,阴影部分扇形的圆心角是36°.
]

答案： 36°

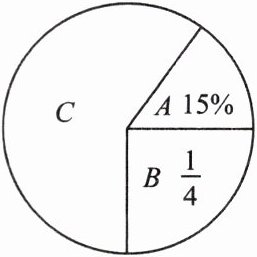
10. 如图,将圆分成 $ A,B,C $ 三个扇形,且半径长为 $ 3 \mathrm{~cm} $.
(1)求扇形 $ C $ 的面积;
(2)求扇形 $ A $ 和 $ B $ 的圆心角的度数.
]

答案：
(1)扇形$C$的圆心角为$360^{\circ}×(1 - 15\%-\frac{1}{4}×100\%)=360^{\circ}×(1 - 0.15 - 0.25)=360^{\circ}×0.6 = 216^{\circ}$。
根据扇形面积公式$S=\frac{n\pi r^{2}}{360}$（$n$为圆心角度数，$r$为半径），已知$r = 3\mathrm{cm}$，$n = 216^{\circ}$，则扇形$C$的面积$S_{C}=\frac{216×\pi×3^{2}}{360}=\frac{216×9\pi}{360}=\frac{27\pi}{5}= 5.4\pi(\mathrm{cm}^{2})$。
(2)已知扇形$A$的圆心角度数占比为$15\%$，所以扇形$A$的圆心角度数$n_{A}=360^{\circ}×15\% = 54^{\circ}$。
因为扇形$B$的圆心角度数占比为$\frac{1}{4}$，所以扇形$B$的圆心角度数$n_{B}=360^{\circ}×\frac{1}{4}=90^{\circ}$。
综上，答案为：
(1)扇形$C$的面积为$5.4\pi\mathrm{cm}^{2}$；
(2)扇形$A$的圆心角为$54^{\circ}$，扇形$B$的圆心角为$90^{\circ}$。

观察探究及应用.
(1) 观察图形并填空:

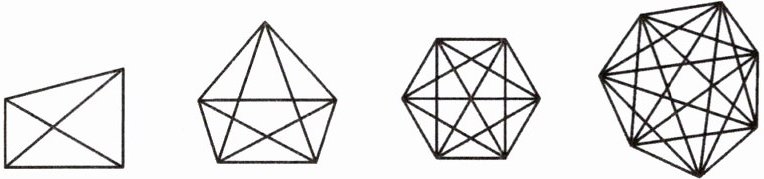
一个四边形有2条对角线;
一个五边形有5条对角线;
一个六边形有9条对角线;
一个七边形有14条对角线.
(2) 分析探究:
由凸 $ n $ 边形的一个顶点出发,可作$n - 3$条对角线,多边形有 $ n $ 个顶点,若允许重复计数,共可作$n(n - 3)$条对角线.
(3) 结论:
一个凸 $ n $ 边形有$\frac{n(n - 3)}{2}$条对角线.
(4) 应用:
一个凸十二边形有54条对角线.

答案：
(1) $2$；$5$；$9$；$14$
(2) $n - 3$；$n(n - 3)$
(3) $\frac{n(n - 3)}{2}$
(4) $54$