第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
1. 平面上有A,B,C三点,经过任意两点画一条直线,可以画出直线的数量为(
A.1条
B.3条
C.1条或3条
D.无数条
C
)A.1条
B.3条
C.1条或3条
D.无数条
答案:
C
2. 如图,已知四条线段a,b,c,d中的一条与挡板另一侧的线段m在同一直线上,请借助直尺判断该线段是(
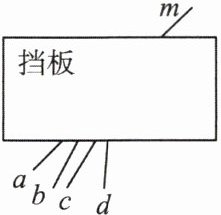
A.a
B.b
C.c
D.d
A
)
A.a
B.b
C.c
D.d
答案:
A
3. 下图中有线段、射线和直线,根据它们的基本特征判断,其中能够相交的是(
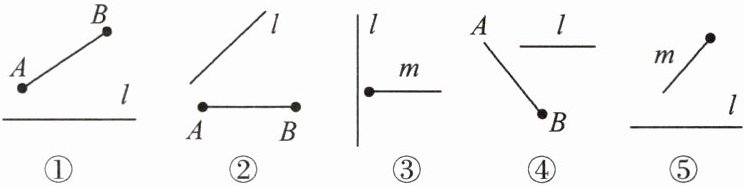
A.①②
B.③④
C.①⑤
D.④⑤
D
)
A.①②
B.③④
C.①⑤
D.④⑤
答案:
D
4. 下列选项中说法正确的是(
A.延长线段AB到C,使BC= AC
B.反向延长线段AB,得到射线BA
C.取直线AB的中点
D.连接A,B两点,并使直线AB经过点C
B
)A.延长线段AB到C,使BC= AC
B.反向延长线段AB,得到射线BA
C.取直线AB的中点
D.连接A,B两点,并使直线AB经过点C
答案:
B
5. 线段有
2
个端点,射线有______1
个端点,直线有______0
个端点.
答案:
2,1,0
6. 平面上有A,B,C三点,过其中的每两点画直线,最多可以画
3
条直线,最少可以画1
条直线.
答案:
3;1
7. 如图,请用两种方式分别表示图①②中的直线、射线、线段.
图① 图②

图① 图②

答案:
图①
直线:直线AB,直线l
射线:射线AB,射线BA
线段:线段AB,线段BA
图②
直线:直线a,直线b,直线AB,直线BA,直线AO,直线OA,直线BO,直线OB
射线:射线OA,射线OB,射线AO,射线BO(以O为端点);射线AB,射线BA(以A、B为端点)
线段:线段OA,线段OB,线段AB,线段AO,线段BO,线段BA
直线:直线AB,直线l
射线:射线AB,射线BA
线段:线段AB,线段BA
图②
直线:直线a,直线b,直线AB,直线BA,直线AO,直线OA,直线BO,直线OB
射线:射线OA,射线OB,射线AO,射线BO(以O为端点);射线AB,射线BA(以A、B为端点)
线段:线段OA,线段OB,线段AB,线段AO,线段BO,线段BA
8. 如图,平面上有四个点A,B,C,D,根据下列语句画图:
(1)在图①中,画线段AC,BD交于E点;
(2)在图①中作射线BC;
(3)在图②中取一点P,使点P既在直线AB上又在直线CD上.
图① 图②

(1)在图①中,画线段AC,BD交于E点;
(2)在图①中作射线BC;
(3)在图②中取一点P,使点P既在直线AB上又在直线CD上.
图① 图②

答案:
(1) 图①:连接A与C,形成线段AC;连接B与D,形成线段BD,两条线段相交于点E。
(2) 图①:从点B向点C方向绘制射线BC。
(3) 图②:点P应位于直线AB与直线CD的交点处。
(1) 图①:连接A与C,形成线段AC;连接B与D,形成线段BD,两条线段相交于点E。
(2) 图①:从点B向点C方向绘制射线BC。
(3) 图②:点P应位于直线AB与直线CD的交点处。
仔细观察下列图案.

(1)如果每过两点可以画一条直线,那么:
第①组最多可以画______条直线,
第②组最多可以画______条直线,
第③组最多可以画______条直线;
(2)探索归纳.
如果平面上有n(n≥3)个点,且每3个点均不在一条直线上,那么最多可以画______条直线;(用含n的式子表示)
(3)解决问题.
某班45名同学在毕业后的一次聚会中,若每两人握手1次问好,那么共需握手______次.

(1)如果每过两点可以画一条直线,那么:
第①组最多可以画______条直线,
第②组最多可以画______条直线,
第③组最多可以画______条直线;
(2)探索归纳.
如果平面上有n(n≥3)个点,且每3个点均不在一条直线上,那么最多可以画______条直线;(用含n的式子表示)
(3)解决问题.
某班45名同学在毕业后的一次聚会中,若每两人握手1次问好,那么共需握手______次.
答案:
3,6,10
@@当平面上有$n(n\geq3)$个点,且每3个点均不在一条直线上时,每个点都能与其他$(n - 1)$个点连成一条直线,这样共能连成$n(n - 1)$条直线。但由于每一条直线都被重复计算了两次(例如点$A$与点$B$连成的直线和点$B$与点$A$连成的直线是同一条),所以最多可以画的直线条数为$\frac{n(n - 1)}{2}$。$\frac{n(n - 1)}{2}$
@@从$45$名同学中选取$2$名同学来握手,这是一个组合问题。组合的计算公式为$C_{n}^{k} = \frac{n!}{k!(n - k)!}$,其中$n$表示总数,$k$表示选取的个数。在本题中$n = 45$,$k = 2$,则:$C_{45}^2=\frac{45!}{2!(45 - 2)!}=\frac{45×44×43!}{2×1×43!}= 990$(次)。故答案为:$990$。
@@当平面上有$n(n\geq3)$个点,且每3个点均不在一条直线上时,每个点都能与其他$(n - 1)$个点连成一条直线,这样共能连成$n(n - 1)$条直线。但由于每一条直线都被重复计算了两次(例如点$A$与点$B$连成的直线和点$B$与点$A$连成的直线是同一条),所以最多可以画的直线条数为$\frac{n(n - 1)}{2}$。$\frac{n(n - 1)}{2}$
@@从$45$名同学中选取$2$名同学来握手,这是一个组合问题。组合的计算公式为$C_{n}^{k} = \frac{n!}{k!(n - k)!}$,其中$n$表示总数,$k$表示选取的个数。在本题中$n = 45$,$k = 2$,则:$C_{45}^2=\frac{45!}{2!(45 - 2)!}=\frac{45×44×43!}{2×1×43!}= 990$(次)。故答案为:$990$。
查看更多完整答案,请扫码查看


