《2025年精练课堂分层作业七年级数学上册北师大版》

5.若$a与b$互为相反数,$c与d$互为倒数,则$a+b+3cd= $3.

答案： 3

6.当$x= 1$时,$2ax^{2}-bx的值为-4$,则当$x= -2$时,$ax^{2}+bx$的值为$-8$.

答案： $-8$（题目是填空题，直接填数值）

7.当$a= 3,b= -1$时,求下列代数式的值.
(1)$(a+b)(a-b)$;
(2)$a^{2}+2ab+b^{2}$.

答案：
(1)
当$a = 3$，$b = -1$时，
$(a + b)(a - b)=(3+( -1))×(3-( -1))=(3 - 1)×(3 + 1)=2×4 = 8$。
(2)
当$a = 3$，$b = -1$时，
$a^{2}+2ab + b^{2}=3^{2}+2×3×(-1)+(-1)^{2}=9-6 + 1=4$。

8.某款手机后置摄像头模组如图所示,其中大圆的半径为$r$,中间小圆的半径为$\frac{1}{2}r$,4个半径为$\frac{1}{5}r$的高清圆形镜头分布在两圆之间.
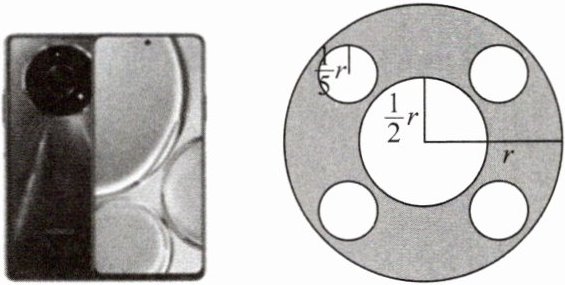
(1)请用含$r$的式子表示图中阴影部分的面积;$\frac{59}{100}\pi r^2$
(2)当$r= 2cm$时,求图中阴影部分的面积.($\pi$取3)$7.08\,cm^2$
]

答案：
(1)$\frac{59}{100}\pi r^2$；
(2)$7.08\,cm^2$

某校七年级3位老师带部分学生去红色旅游,联系了甲、乙两家旅行社.甲旅行社说:“老师免费,学生打八折.”乙旅行社说:“包括老师在内全部打七折.”已知全程费用为每人240元.
(1)设有$x$名学生参加活动,请分别写出参加两家旅行社的费用的代数式;
(2)若有20名学生参加活动,选择哪家旅行社更合算?

答案：
(1)
甲旅行社：老师免费，学生每人费用为$240 × 0.8 = 192$（元），$x$名学生总费用为$192x$元，代数式为$192x$；
乙旅行社：总人数为$(3 + x)$人，每人费用为$240× 0.7 = 168$（元），总费用代数式为$168(x + 3)$。
(2)
当$x = 20$时，
甲旅行社费用：$192×20 = 3840$（元）；
乙旅行社费用：$168×(20 + 3)=168×23 = 3864$（元）。
因为$3840\lt 3864$，所以选择甲旅行社更合算。