《2025年精练课堂分层作业七年级数学上册北师大版》

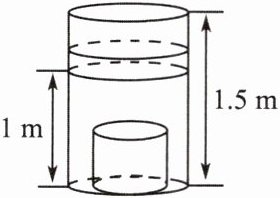
7. 如图,一圆柱形容器的底面半径为 0.5 m,高为 1.5 m,里面盛有 1 m 深的水,将底面半径为 0.3 m、高为 0.5 m 的圆柱形铁块沉入水中,则容器内水面将升高多少米？

答案： 设容器内水面将升高$x$米。
铁块体积：$V_{铁}=πr_{铁}^{2}h_{铁}=π×0.3^{2}×0.5$
水面上升体积：$V_{升}=πr_{容}^{2}x=π×0.5^{2}x$
由$V_{铁}=V_{升}$，得：$π×0.3^{2}×0.5=π×0.5^{2}x$
两边同除以$π$：$0.3^{2}×0.5=0.5^{2}x$
计算：$0.09×0.5=0.25x$，即$0.045=0.25x$
解得：$x=0.045÷0.25=0.18$
答：容器内水面将升高$0.18$米。

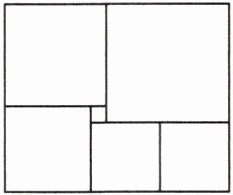
1. 右图是由六个正方形拼成的一个长方形.已知最小的正方形的面积为 1,则此长方形的面积是143。

答案： 143

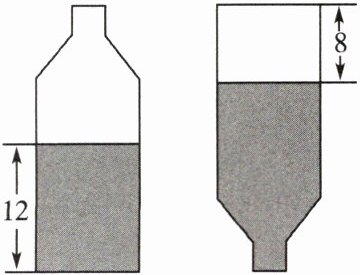
2. 如图,一个饮料瓶的容积为 500 mL,瓶子内还剩有一些饮料.当瓶子正放时,瓶内饮料的高度为 12 cm；倒放时,空余部分的高度为 8 cm,则瓶子的底面积为25 $ \mathrm { cm } ^ { 2 } $。($ 1 \mathrm { mL } = 1 \mathrm { cm } ^ { 3 } $)

答案： 25

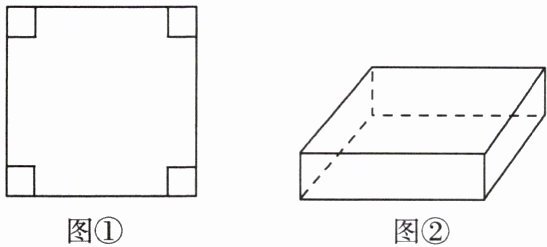
3. 如图①,在边长为 18 cm 的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个如图②的无盖长方体.设剪去的小正方形的边长为 4 cm,则这样折成的无盖长方体的容积是$400cm^3$。

答案： $400cm^3$

4. 小张用 10 m 长的篱笆在墙边围成一个长方形鸡棚(鸡棚的一边长靠墙),使长比宽长 5 m,但在宽的一边有一扇 1 m 的门.求围成的鸡棚的长和宽。

答案： 鸡棚的长为7米，宽为2米。