第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
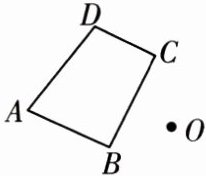
6. 如图,以点 $ O $ 为位似中心,将四边形 $ ABCD $ 放大为原来的 $ 2 $ 倍(只需画出一种情况即可).

答案:
6.如图所示,四边形A′B′C′D′即为所求作(答案不唯一)

6.如图所示,四边形A′B′C′D′即为所求作(答案不唯一)

7. [2024 长春模拟]如图,已知$\triangle A'B'C'$与$\triangle ABC$是以点 $ O $ 为位似中心的位似图形,位似比为 $ 2:3 $,则下列说法错误的是(
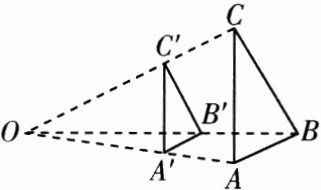
A.$\triangle BCO\sim\triangle B'C'O$
B.$\triangle A'B'C'$与$\triangle ABC$的周长比为 $ 2:3 $
C.$ S_{\triangle A'B'C'}:S_{\triangle ABC}=4:9 $
D.$ OB':BB' = 3:2 $
D
)
A.$\triangle BCO\sim\triangle B'C'O$
B.$\triangle A'B'C'$与$\triangle ABC$的周长比为 $ 2:3 $
C.$ S_{\triangle A'B'C'}:S_{\triangle ABC}=4:9 $
D.$ OB':BB' = 3:2 $
答案:
7.D
8. 如图,图中的小方格都是边长为 $ 1 $ 的正方形,$\triangle ABC$与$\triangle A'B'C'$是关于点 $ O $ 为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点 $ O $;
(2)求出$\triangle ABC$与$\triangle A'B'C'$的相似比.
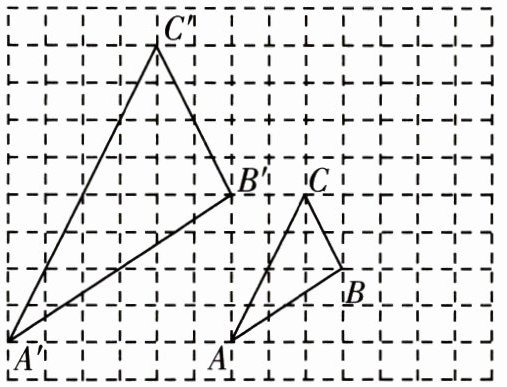
(1)画出位似中心点 $ O $;
(2)求出$\triangle ABC$与$\triangle A'B'C'$的相似比.
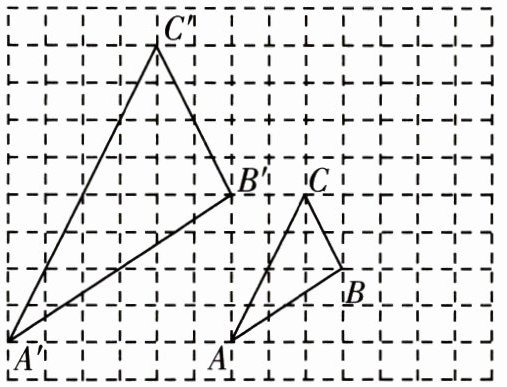
答案:
8.
(1)如图所示,点O即为所求作

(2)△ABC与△A′B′C′的相似比为$\frac{1}{2}$
8.
(1)如图所示,点O即为所求作

(2)△ABC与△A′B′C′的相似比为$\frac{1}{2}$
9. (1)如图①,将$\triangle ABC$放大为原来的 $ 2 $ 倍,且位似中心为$\triangle ABC$左侧的点 $ O $(只需画出一种情况即可);
(2)如图②,将四边形 $ ABCD $ 缩小到原来的$\frac{1}{2}$,且位似中心为图形内部的点 $ O $(只需画出一种情况即可).
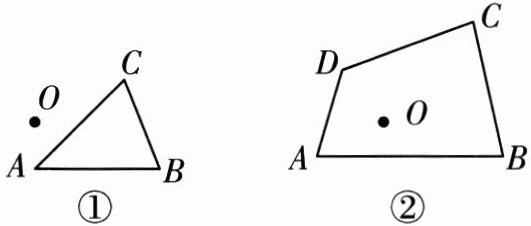
(2)如图②,将四边形 $ ABCD $ 缩小到原来的$\frac{1}{2}$,且位似中心为图形内部的点 $ O $(只需画出一种情况即可).
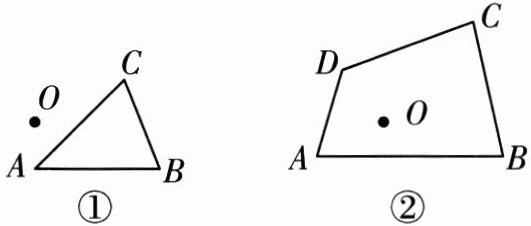
答案:
9.
(1)
(2)如图所示(答案不唯一)

9.
(1)
(2)如图所示(答案不唯一)

10. 【几何直观】如图,在边长为 $ 1 $ 个单位长度的小正方形组成的网格中,按要求画出$\triangle A_1B_1C_1$和$\triangle A_2B_2C_2$.
(1)把$\triangle ABC$先向右平移 $ 4 $ 个单位长度,再向上平移 $ 1 $ 个单位长度,得到$\triangle A_1B_1C_1$;
(2)以图中的点 $ O $ 为位似中心,将$\triangle A_1B_1C_1$作位似变换且放大为原来的 $ 2 $ 倍,得到$\triangle A_2B_2C_2$;
(3)填空:$\frac{S_{\triangle ABC}}{S_{\triangle A_2B_2C_2}}=$

(1)把$\triangle ABC$先向右平移 $ 4 $ 个单位长度,再向上平移 $ 1 $ 个单位长度,得到$\triangle A_1B_1C_1$;
(2)以图中的点 $ O $ 为位似中心,将$\triangle A_1B_1C_1$作位似变换且放大为原来的 $ 2 $ 倍,得到$\triangle A_2B_2C_2$;
(3)填空:$\frac{S_{\triangle ABC}}{S_{\triangle A_2B_2C_2}}=$
$\frac{1}{4}$
.
答案:
10.
(1)
(2)如图所示

(3)$\frac{1}{4}$
10.
(1)
(2)如图所示

(3)$\frac{1}{4}$
查看更多完整答案,请扫码查看


