《2025年全效学习同步学练测九年级数学上册湘教版》

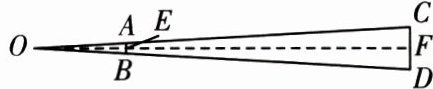
7. 如图为步枪在瞄准时的示意图，$AB// CD$，从眼睛 $O$ 到准星的距离 $OE$ 为 $80$ cm，眼睛到目标 $F$ 的距离 $OF$ 为 $200$ m，步枪上准星宽度 $AB$ 为 $2$ mm. 若射击时，由于抖动导致视线偏离了准星上点 $E$ $1$ mm，则目标偏离的距离为(A)


A.$25$ cm
B.$50$ cm
C.$75$ cm
D.$100$ cm

答案： 7.A

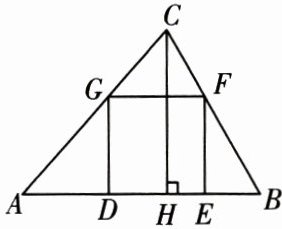
8. 如图，在 $\triangle ABC$ 中，$CH\perp AB$，$CH = h$，$AB = c$. 若内接正方形 $DEFG$ 的边长是 $x$，则 $h$，$c$，$x$ 之间的数量关系为(D)

A.$x^{2}+h^{2}=c^{2}$
B.$\frac{1}{2}x + h = c$
C.$h^{2}=xc$
D.$\frac{1}{x}=\frac{1}{h}+\frac{1}{c}$

答案： 8.D

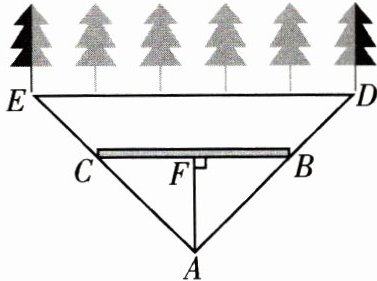
9. [2024 娄底模拟]如图，某宣传栏 $BC$ 后面 $1$ m 处植有与宣传栏平行的 $6$ 棵树，即 $DE// BC$，且相邻两棵树干之间的间隔均为 $1$ m. 一人站在宣传栏前面的点 $A$ 处正好看 到两端的树干，其余的 $4$ 棵树均被宣传栏挡住. 已知 $AF\perp BC$，$AF=\frac{3}{2}$ m，求宣传栏 $BC$ 的长(不计宣传栏的厚度).

答案： 9.宣传栏BC的长是3m

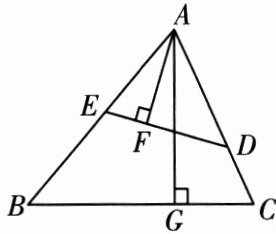
10. 【推理能力】如图，在锐角三角形 $ABC$ 中，点 $D$，$E$ 分别在 $AC$，$AB$ 上，$AG\perp BC$ 于点 $G$，$AF\perp DE$ 于点 $F$，$\angle EAF=\angle GAC$.
(1) 求证：$\triangle AEF\backsim\triangle ACG$；
(2) 求证：$\angle ADE=\angle B$；
(3) 若 $AD = 3$，$AB = 5$，求 $\frac{AF}{AG}$ 的值.

答案： 1. （1）证明：
因为$AG\perp BC$，$AF\perp DE$，所以$\angle AFE=\angle AGC = 90^{\circ}$。
又已知$\angle EAF=\angle GAC$。
根据两角分别相等的两个三角形相似，在$\triangle AEF$和$\triangle ACG$中，$\left\{\begin{array}{l}\angle AFE=\angle AGC\\\angle EAF=\angle GAC\end{array}\right.$，所以$\triangle AEF\backsim\triangle ACG$。
2. （2）证明：
由（1）知$\triangle AEF\backsim\triangle ACG$，所以$\angle AED=\angle ACB$。
在$\triangle ADE$和$\triangle ABC$中，$\angle A=\angle A$（公共角），$\angle AED=\angle ACB$。
根据两角分别相等的两个三角形相似，可得$\triangle ADE\backsim\triangle ABC$。
再根据相似三角形的对应角相等，所以$\angle ADE=\angle B$。
3. （3）解：
由（1）知$\triangle AEF\backsim\triangle ACG$，所以$\frac{AF}{AG}=\frac{AE}{AC}$。
又因为$\triangle ADE\backsim\triangle ABC$，根据相似三角形对应边成比例，可得$\frac{AD}{AB}=\frac{AE}{AC}$。
已知$AD = 3$，$AB = 5$，所以$\frac{AF}{AG}=\frac{AD}{AB}=\frac{3}{5}$。
综上，（1）得证$\triangle AEF\backsim\triangle ACG$；（2）得证$\angle ADE=\angle B$；（3）$\frac{AF}{AG}$的值为$\frac{3}{5}$。