第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
5. 某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度 $ y $(μg/mL)与服药时间 $ x $(h)之间函数关系如图所示,则血液中药物浓度不低于 $ 4 $ μg/mL 的持续时间为(
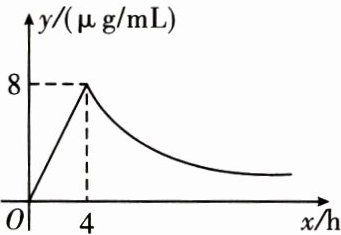
A.$ 4 $ h
B.$ 6 $ h
C.$ 8 $ h
D.$ 10 $ h
B
)
A.$ 4 $ h
B.$ 6 $ h
C.$ 8 $ h
D.$ 10 $ h
答案:
5.B
6. [2023 宁夏]给某气球充满一定质量的气体,在温度不变时,气球内气体的气压 $ p $(KPa)是气体体积 $ V $(m³)的反比例函数,其图象如图所示.
(1)当气球内的气压超过 $ 150 $ KPa 时,气球会爆炸,若将气球近似看成一个球体,试估计气球的半径至少为多少时气球不会爆炸(球体的体积公式 $ V=\frac{4}{3}\pi r^3 $,$ \pi $ 取 $ 3 $);
(2)请你利用 $ p $ 与 $ V $ 的关系试着解释为什么超载的车辆容易爆胎.
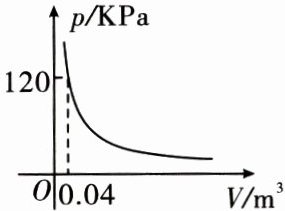
(1)当气球内的气压超过 $ 150 $ KPa 时,气球会爆炸,若将气球近似看成一个球体,试估计气球的半径至少为多少时气球不会爆炸(球体的体积公式 $ V=\frac{4}{3}\pi r^3 $,$ \pi $ 取 $ 3 $);
(2)请你利用 $ p $ 与 $ V $ 的关系试着解释为什么超载的车辆容易爆胎.

答案:
6.
(1)气球的半径至少为0.2m时,气球不会爆炸
(2)车辆超载,会导致轮胎体积变小,则胎内气压会增大,从而导致爆胎
(1)气球的半径至少为0.2m时,气球不会爆炸
(2)车辆超载,会导致轮胎体积变小,则胎内气压会增大,从而导致爆胎
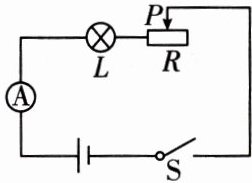
7.【应用意识】在一次物理实验中,小冉同学用一固定电压为 $ 12 $ V 的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡 $ L $(灯丝的阻值 $ R_L=2 $ Ω)亮度的实验(如图).已知串联电路中,电流与电阻 $ R $,$ R_L $ 之间关系为 $ I=\frac{U}{R+R_L} $,通过实验得出如下数据:

(1)$ a= $
(2)根据以上实验,构建出函数 $ y=\frac{12}{x+2} $($ x \ge 0 $),结合表格信息,探究函数 $ y=\frac{12}{x+2} $($ x \ge 0 $)的图象与性质.
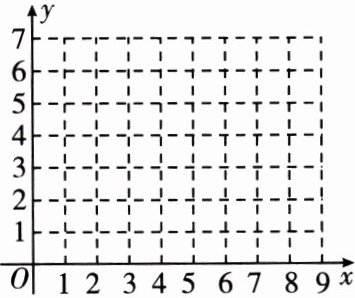
①在如图所示的平面直角坐标系中画出对应函数 $ y=\frac{12}{x+2} $($ x \ge 0 $)的图象;
②随着自变量 $ x $ 的不断增大,函数值 $ y $ 的变化趋势是
(3)结合(2)中函数图象分析,当 $ x \ge 0 $ 时,不等式 $ \frac{12}{x+2} \ge -\frac{3}{2}x+6 $ 的解集为

(1)$ a= $
2
,$ b= $1.5
.(2)根据以上实验,构建出函数 $ y=\frac{12}{x+2} $($ x \ge 0 $),结合表格信息,探究函数 $ y=\frac{12}{x+2} $($ x \ge 0 $)的图象与性质.
①在如图所示的平面直角坐标系中画出对应函数 $ y=\frac{12}{x+2} $($ x \ge 0 $)的图象;
②随着自变量 $ x $ 的不断增大,函数值 $ y $ 的变化趋势是
不断减小
.(3)结合(2)中函数图象分析,当 $ x \ge 0 $ 时,不等式 $ \frac{12}{x+2} \ge -\frac{3}{2}x+6 $ 的解集为
$x\geq2$或$x=0$
.

答案:
7.
(1)2 1.5
(2)①如图所示

②不断减小
(3)$x\geq2$或$x=0$
7.
(1)2 1.5
(2)①如图所示

②不断减小
(3)$x\geq2$或$x=0$
查看更多完整答案,请扫码查看


