《2025年全效学习同步学练测九年级数学上册湘教版》

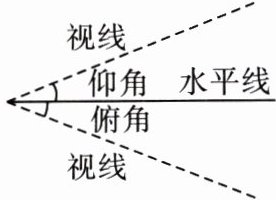
如图，在视线与水平线所成的角中，视线在水平线上方的叫作仰角，视线在水平线下方的叫作俯角.

答案： 上方 下方

例 如图，平地上两栋建筑物 $ CD $ 和 $ AB $ 相距 $ 36 $ m，小敏在建筑物 $ CD $ 的阳台 $ E $ 处测得建筑物 $ AB $ 底部 $ B $ 的俯角为 $ 45^{\circ} $，顶部 $ A $ 的仰角为 $ 33^{\circ} $. 求建筑物 $ AB $ 的高度.（结果保留整数. 参考数据：$ \sin 33^{\circ} \approx 0.54 $，$ \cos 33^{\circ} \approx 0.84 $，$ \tan 33^{\circ} \approx 0.65 $）

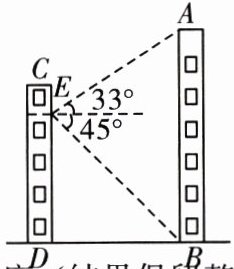
【思路分析】过点 $ E $ 作 $ EF \perp AB $，构造直角三角形，在 $ Rt \triangle AEF $ 和 $ Rt \triangle BEF $ 中分别求出 $ AF $ 和 $ BF $ 的长即可.

答案： 过点 $ E $ 作 $ EF \perp AB $，垂足为 $ F $。
在 $ Rt \triangle AEF $ 中，$ \angle AEF = 33° $，$ EF = 36 $ m，
$ \therefore AF = EF \cdot \tan 33° \approx 36 × 0.65 = 23.4 (m) $，
在 $ Rt \triangle BEF $ 中，$ \angle BEF = 45° $，$ EF = 36 $ m，
$ \therefore BF = EF = 36 (m) $，
$ \therefore AB = AF + BF = 23.4 + 36 \approx 59 (m) $。
答：建筑物 $ AB $ 的高度约为 $ 59 $ m。

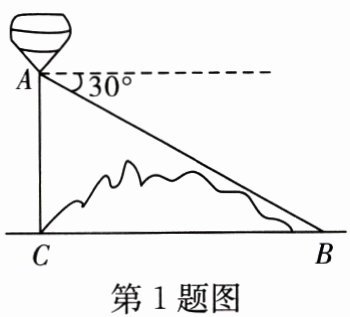
1. 如图，某地修建高速公路，要从 $ B $ 地向 $ C $ 地修一条隧道(点 $ B $，$ C $ 在同一水平线上). 为了测量 $ B $，$ C $ 两地之间的距离，某工程师乘坐热气球从 $ C $ 地出发，垂直上升 $ 100 $ m 到达 $ A $ 处，在 $ A $ 处观察 $ B $ 地的俯角为 $ 30^{\circ} $，则 $ B $，$ C $ 两地之间的距离为(A)

A.$ 100\sqrt{3} $ m
B.$ 50\sqrt{2} $ m
C.$ 50\sqrt{3} $ m
D.$ \dfrac{100\sqrt{3}}{3} $ m

答案： 1.A

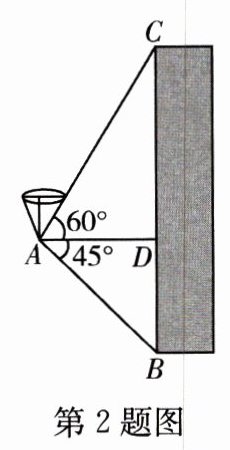
2. [2024 绥化] 如图，用热气球的探测器测一栋楼的高度，从热气球上的点 $ A $ 测得该楼顶部点 $ C $ 的仰角为 $ 60^{\circ} $，测得底部点 $ B $ 的俯角为 $ 45^{\circ} $，点 $ A $ 与楼 $ BC $ 的水平距离 $ AD = 50 $ m，则这栋楼的高度为(50+50\sqrt{3})m(结果保留根号).

答案： $2.(50+50\sqrt{3})$

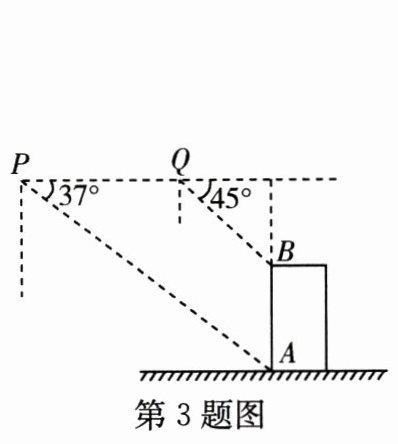
3. [2024 盐城] 如图，小明用无人机测量教学楼的高度，将无人机垂直上升距地面 $ 30 $ m 的点 $ P $ 处，测得教学楼底端点 $ A $ 的俯角为 $ 37^{\circ} $，再将无人机沿教学楼方向水平飞行 $ 26.6 $ m 至点 $ Q $ 处，测得教学楼顶端点 $ B $ 的俯角为 $ 45^{\circ} $，则教学楼 $ AB $ 的高度约为17m.(精确到 $ 1 $ m. 参考数据：$ \sin 37^{\circ} \approx 0.60 $，$ \cos 37^{\circ} \approx 0.80 $，$ \tan 37^{\circ} \approx 0.75 $)

答案： 3.17

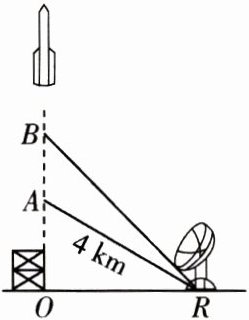
4. [2024 娄底模拟] 如图，一枚运载火箭从地面 $ O $ 处发射，当火箭到达点 $ A $ 处时. 地面 $ R $ 处的雷达站测得 $ AR $ 的距离是 $ 4 $ km，仰角为 $ 30^{\circ} $. $ 5 $ s 后，火箭直线上升到达点 $ B $ 处，此时地面 $ R $ 处的雷达站测得 $ B $ 处的仰角为 $ 45^{\circ} $. 求火箭从 $ A $ 到 $ B $ 处的平均速度（结果精确到 $ 1 $ m/s. 参考数据：$ \sqrt{3} \approx 1.732 $）.

答案： 4.火箭从A处到B处的平均速度约为293m/s