《2025年初中必刷题八年级数学上册华师大版》

1 [2025北京房山区期末,中]实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )


A.$-b＞a＞0$
B.$b＞-a＞1$
C.$b＜-a＜-1$
D.$-a＜b＜-2$

答案： A [解析]
∵−2＜b＜−1,
∴1＜−b＜2. 又
∵0＜a＜1,
∴−b＞a＞0,
∴A选项正确，符合题意.
∵0＜a＜1,
∴−1＜−a＜0,
∴b＜−a＜0,
∴B选项错误，不符合题意;C选项错误，不符合题意;D选项错误，不符合题意. 故选A.

2 [中]已知7个实数$-\sqrt {5},\frac {3}{2},4,5.\dot {3},-\sqrt [3]{64},0,π$.其中3个数在如图所示的数轴上分别用点A,B,C表示.

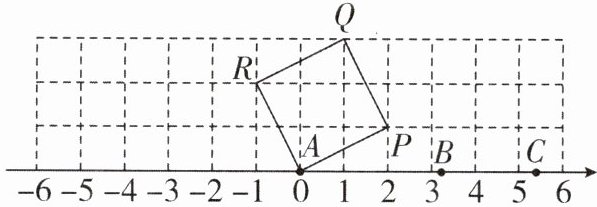
(1)点A表示数____,点B表示数____,点C表示数____.
(2)在数轴上精确地表示出剩下的4个数(提示:注意观察正方形APQR的面积),并将所有的数用“＜”连接.

答案：
[解]
(1)根据点A,B,C在数轴上的位置，可知点A表示数0，点B表示数π，点C表示数$5.\dot{3}. $故答案为$0,π,5.\dot{3}.(2)$如图所示即为所求作. 由数轴可知，$-\sqrt[3]{64}$＜-\sqrt{5}＜0＜\frac{3}{2}＜π＜4＜5.\dot{3}.

3 [2025湖北孝感期中,中]比较大小:$\sqrt {10}$____3;$\sqrt [3]{-25}$____-3.

答案： ＞　＞　[解析]
∵$\sqrt{10}＞\sqrt{9}$，
∴$\sqrt{10}＞3$.
∵$\sqrt[3]{-25}＞\sqrt[3]{-27}$，
∴$\sqrt[3]{-25}＞-3$.

4 新考向传统文化[2024安徽中考]我国古代数学家张衡将圆周率取值为$\sqrt {10}$,祖冲之给出圆周率的一种分数形式的近似值为$\frac {22}{7}$.比较大小:$\sqrt {10}$____$\frac {22}{7}$(填“＞”或“＜”).

答案： ＞ [解析]($\sqrt{10}$)² = 10，($\frac{22}{7}$)² = $\frac{484}{49}$，
∵10 ＞ $\frac{484}{49}$，
∴$\sqrt{10}＞\frac{22}{7}$，故答案为＞.

5 [中]比较大小:$-\sqrt {2.1}$____$-\frac {3}{2}$.(填“＞”“＜”或“=”)

答案： ＞ [解析]
∵(−$\sqrt{2.1}$)² = 2.1，(−$\frac{3}{2}$)² = $\frac{9}{4}$ = 2.25，2.25 ＞ 2.1，
∴−$\sqrt{2.1}＞-\frac{3}{2}$.

6 [中]设$A= 3x^{2}-3x+5,B= 2x^{2}-3x-2$,若x取任意实数,则A与B的大小关系为( )

A.$A＞B$
B.$A＜B$
C.$A= B$
D.无法比较

答案： A [解析]A - B = (3x² - 3x + 5) - (2x² - 3x - 2) = 3x² - 3x + 5 - 2x² + 3x + 2 = x² + 7.
∵不论x为何值，x² ≥ 0，
∴x² + 7 ＞ 0，
∴A - B ＞ 0，
∴A ＞ B，故选A.

7 [中]阅读材料:对于任意两个实数a和b比较大小,若$a-b＞0$,则$a＞b$;若$a-b= 0$,则$a= b$;若$a-b＜0$,则$a＜b$.上面的规律反过来也成立.参考材料,解决问题:
(1)比较大小:$3+\sqrt {5}$____$\sqrt {10}+\sqrt {5}$;(填“＜”“=”或“＞”)
(2)已知$2y-2= x$,且$x≥0$,若$A= 5xy+y+1,B= 5xy+2y$,试比较A和B的大小.

答案： [解]
(1)3 + $\sqrt{5}$ - ($\sqrt{10}+\sqrt{5}$) = 3 + $\sqrt{5}$ - $\sqrt{10}$ - $\sqrt{5}$ = 3 - $\sqrt{10}$.
∵3 - $\sqrt{10}$ ＜ 0，
∴3 + $\sqrt{5}$ - ($\sqrt{10}+\sqrt{5}$) ＜ 0，
∴3 + $\sqrt{5}$ ＜ $\sqrt{10}+\sqrt{5}$，故答案为＜.
(2)
∵x = 2y - 2，x ≥ 0，
∴2y - 2 ≥ 0，
∴y - 1 ≥ 0，
∴ - y + 1 ≤ 0.
∵A - B = (5xy + y + 1) - (5xy + 2y) = - y + 1 ≤ 0，
∴A ≤ B.

8 [中]比较$4,\sqrt {17},\sqrt [3]{63}$的大小,正确的是( )

A.$\sqrt [3]{63}＜4＜\sqrt {17}$
B.$4＜\sqrt [3]{63}＜\sqrt {17}$
C.$4＜\sqrt {17}＜\sqrt [3]{63}$
D.$\sqrt {17}＜\sqrt [3]{63}＜4$

答案： A [解析]
∵4 = $\sqrt{16}＜\sqrt{17}$，4 = $\sqrt[3]{64}＞\sqrt[3]{63}$，
∴$\sqrt[3]{63}＜4＜\sqrt{17}$，故选A.

9 [2025浙江宁波质检,中]比较$\sqrt {37}-2与\sqrt {3}+2$的大小.

答案： [解]
∵$\sqrt{36}＜\sqrt{37}＜\sqrt{49}$，
∴6 ＜ $\sqrt{37}$ ＜ 7，
∴$\sqrt{37}-2＞4$. 又
∵$\sqrt{1}＜\sqrt{3}＜\sqrt{4}$，
∴1 ＜ $\sqrt{3}$ ＜ 2，
∴$\sqrt{3}+2＜4$，
∴$\sqrt{37}-2＞\sqrt{3}+2$.