第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
一、选择题(每小题5分,共15分)
1有下列各数:$\frac{\pi}{2},\sqrt[3]{9},\sqrt{\frac{1}{144}},\frac{22}{7},0.303003,\frac{\sqrt{2}}{2}$,其中无理数的个数为 ( )
A.2
B.3
C.4
D.5
1有下列各数:$\frac{\pi}{2},\sqrt[3]{9},\sqrt{\frac{1}{144}},\frac{22}{7},0.303003,\frac{\sqrt{2}}{2}$,其中无理数的个数为 ( )
A.2
B.3
C.4
D.5
答案:
B 【解析】$\sqrt{\frac{1}{144}}=\frac{1}{12}$,$\frac{22}{7}$是分数,属于有理数;0.303003 是有限小数,属于有理数;无理数有$\frac{\pi}{2}$,$\sqrt[3]{9}$,$\frac{\sqrt{2}}{2}$,共 3 个. 故选 B.
2[2025四川成都青羊区质检]下列说法正确的是 ( )
A.-4的平方根是±2
B.$\sqrt{16}$的算术平方根是4
C.平方根等于本身的数是0和1
D.0的平方根与算术平方根都是0
A.-4的平方根是±2
B.$\sqrt{16}$的算术平方根是4
C.平方根等于本身的数是0和1
D.0的平方根与算术平方根都是0
答案:
D 【解析】负数没有平方根,则 A 选项不符合题意;$\sqrt{16}$的算术平方根是 2,则 B 选项不符合题意;平方根等于本身的数是 0,则 C 选项不符合题意;0 的平方根与算术平方根都是 0,则 D 选项符合题意. 故选 D.
3如图所示的数轴上,点C与点B关于点A对称,A,B两点对应的实数分别是1和$\sqrt{5}$,则点C对应的实数是 ( )
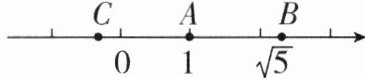
A.$1-\sqrt{5}$
B.$\sqrt{5}-2$
C.$-\sqrt{5}$
D.$2-\sqrt{5}$

A.$1-\sqrt{5}$
B.$\sqrt{5}-2$
C.$-\sqrt{5}$
D.$2-\sqrt{5}$
答案:
D 【解析】
∵ A,B 两点对应的实数分别是 1 和$\sqrt{5}$,
∴ $AB=\sqrt{5}-1$. 又
∵ 点 C 与点 B 关于点 A 对称,
∴ $AC=AB$. 设点 C 所表示的数为 c,则$AC=1-c$,
∴ $1-c=\sqrt{5}-1$,
∴ $c=2-\sqrt{5}$,故选 D.
∵ A,B 两点对应的实数分别是 1 和$\sqrt{5}$,
∴ $AB=\sqrt{5}-1$. 又
∵ 点 C 与点 B 关于点 A 对称,
∴ $AC=AB$. 设点 C 所表示的数为 c,则$AC=1-c$,
∴ $1-c=\sqrt{5}-1$,
∴ $c=2-\sqrt{5}$,故选 D.
二、填空题(每小题5分,共20分)
4[2025贵州毕节期末]如果正数a + 1的平方根是±2,b + 4的立方根是-2,则$|a + b|$的算术平方根是____.
4[2025贵州毕节期末]如果正数a + 1的平方根是±2,b + 4的立方根是-2,则$|a + b|$的算术平方根是____.
答案:
3 【解析】
∵ 正数 a+1 的平方根是±2,b+4 的立方根是 -2,
∴ a+1=4,b+4=-8,
∴ a=3,b=-12,则$|a+b|=|3+(-12)|=9$,
∴ $|a+b|$的算术平方根是 3.
∵ 正数 a+1 的平方根是±2,b+4 的立方根是 -2,
∴ a+1=4,b+4=-8,
∴ a=3,b=-12,则$|a+b|=|3+(-12)|=9$,
∴ $|a+b|$的算术平方根是 3.
5[2025四川成都期中]比较大小:$\frac{\sqrt{5}-1}{2}$____$\frac{1}{2}$(填“>”“<”或“=”).
答案:
> 【解析】
∵ $2 < \sqrt{5} < 3$,
∴ $1 < \sqrt{5}-1 < 2$,
∴ $\frac{1}{2} < \frac{\sqrt{5}-1}{2} < 1$,故$\frac{\sqrt{5}-1}{2} > \frac{1}{2}$,故答案为>.
∵ $2 < \sqrt{5} < 3$,
∴ $1 < \sqrt{5}-1 < 2$,
∴ $\frac{1}{2} < \frac{\sqrt{5}-1}{2} < 1$,故$\frac{\sqrt{5}-1}{2} > \frac{1}{2}$,故答案为>.
6[2025山西太原质检]已知$10+\sqrt{3}= x + y$,其中x是整数,0<y<1,则x - y的相反数为____.
答案:
$-12+\sqrt{3}$ 【解析】
∵ $1 < 3 < 4$,
∴ $\sqrt{1} < \sqrt{3} < \sqrt{4}$,即$1 < \sqrt{3} < 2$,
∴ $11 < 10+\sqrt{3} < 12$.
∵ $10+\sqrt{3}=x+y$,其中 x 是整数,$0 < y < 1$,
∴ x=11,$y=10+\sqrt{3}-11=\sqrt{3}-1$,
∴ $x-y=11-\sqrt{3}+1=12-\sqrt{3}$,
∴ x-y 的相反数为$-(12-\sqrt{3})=-12+\sqrt{3}$,故答案为$-12+\sqrt{3}$.
∵ $1 < 3 < 4$,
∴ $\sqrt{1} < \sqrt{3} < \sqrt{4}$,即$1 < \sqrt{3} < 2$,
∴ $11 < 10+\sqrt{3} < 12$.
∵ $10+\sqrt{3}=x+y$,其中 x 是整数,$0 < y < 1$,
∴ x=11,$y=10+\sqrt{3}-11=\sqrt{3}-1$,
∴ $x-y=11-\sqrt{3}+1=12-\sqrt{3}$,
∴ x-y 的相反数为$-(12-\sqrt{3})=-12+\sqrt{3}$,故答案为$-12+\sqrt{3}$.
7[2025浙江杭州期中]$\sqrt[3]{128x}$是一个正整数,则满足条件的最小正整数x的值是____.
答案:
4 【解析】
∵ $\sqrt[3]{128x}$是一个正整数,
∴ x>0,128x 能完全开立方.
∵ $128x=2^3×4^2x$,
∴ 满足条件的最小正整数 x 的值为 4. 故答案为 4.
∵ $\sqrt[3]{128x}$是一个正整数,
∴ x>0,128x 能完全开立方.
∵ $128x=2^3×4^2x$,
∴ 满足条件的最小正整数 x 的值为 4. 故答案为 4.
8(1)[2024北京大兴区期末]计算:$|1-\sqrt{3}|+\sqrt[3]{-8}+\sqrt{16}$.
(2)[2024重庆永川区期末]计算:$|-\sqrt{9}|+\sqrt[3]{-8}-\sqrt{\frac{1}{4}}+|\frac{1}{2}-\sqrt{2}|+\sqrt{(-\sqrt{2})^2}$.
(2)[2024重庆永川区期末]计算:$|-\sqrt{9}|+\sqrt[3]{-8}-\sqrt{\frac{1}{4}}+|\frac{1}{2}-\sqrt{2}|+\sqrt{(-\sqrt{2})^2}$.
答案:
【解】
(1)$|1-\sqrt{3}|+\sqrt[3]{-8}+\sqrt{16}=\sqrt{3}-1-2+4=\sqrt{3}+1$.
(2)原式$=3-2-\frac{1}{2}+\sqrt{2}-\frac{1}{2}+\sqrt{2}=2\sqrt{2}$.
(1)$|1-\sqrt{3}|+\sqrt[3]{-8}+\sqrt{16}=\sqrt{3}-1-2+4=\sqrt{3}+1$.
(2)原式$=3-2-\frac{1}{2}+\sqrt{2}-\frac{1}{2}+\sqrt{2}=2\sqrt{2}$.
9[2025吉林长春质检]解答下列各题:
(1)已知$(x - 2)^2+\sqrt{y - x + 1}= 0$,求x + 2y的平方根.
(2)已知x,y为实数,且$y= \sqrt{x - 9}-\sqrt{9 - x}+4$,求$\sqrt{x}+\sqrt{y}$的值.
(1)已知$(x - 2)^2+\sqrt{y - x + 1}= 0$,求x + 2y的平方根.
(2)已知x,y为实数,且$y= \sqrt{x - 9}-\sqrt{9 - x}+4$,求$\sqrt{x}+\sqrt{y}$的值.
答案:
【解】
(1)
∵ $(x-2)^2+\sqrt{y-x+1}=0$,$(x-2)^2\geq0$,$\sqrt{y-x+1}\geq0$,
∴ x-2=0,y-x+1=0,
∴ x=2,
∴ y-2+1=0,
∴ y=1,
∴ x+2y=2+2×1=4,
∴ x+2y 的平方根是$\pm\sqrt{4}=\pm2$.
(2)
∵ $y=\sqrt{x-9}-\sqrt{9-x}+4$,
∴ $\begin{cases}x-9\geq0\\9-x\geq0\end{cases}$解得x=9,
∴ $y=\sqrt{9-9}-\sqrt{9-9}+4=4$,
∴ $\sqrt{x}+\sqrt{y}=\sqrt{9}+\sqrt{4}=3+2=5$.
(1)
∵ $(x-2)^2+\sqrt{y-x+1}=0$,$(x-2)^2\geq0$,$\sqrt{y-x+1}\geq0$,
∴ x-2=0,y-x+1=0,
∴ x=2,
∴ y-2+1=0,
∴ y=1,
∴ x+2y=2+2×1=4,
∴ x+2y 的平方根是$\pm\sqrt{4}=\pm2$.
(2)
∵ $y=\sqrt{x-9}-\sqrt{9-x}+4$,
∴ $\begin{cases}x-9\geq0\\9-x\geq0\end{cases}$解得x=9,
∴ $y=\sqrt{9-9}-\sqrt{9-9}+4=4$,
∴ $\sqrt{x}+\sqrt{y}=\sqrt{9}+\sqrt{4}=3+2=5$.
10根据下表回答下列问题:
|x|17|17.1|17.2|17.3|17.4|17.5|
|$x^2$|289|292.41|295.84|299.29|302.76|306.25|
|x|17.6|17.7|17.8|17.9|18|
|$x^2$|309.76|313.29|316.84|320.41|324|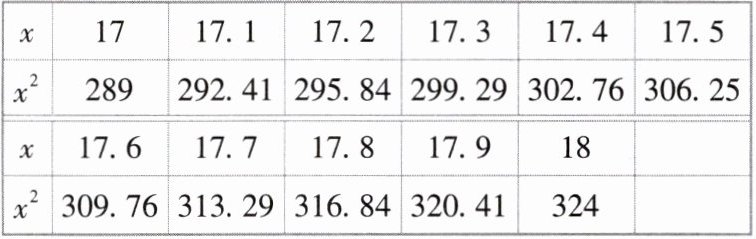
(1)316.84的平方根是____;$\sqrt{299.3}\approx$____;$\sqrt{29241}= $____.
(2)若$\sqrt{n}$介于17.6与17.7之间,则满足条件的整数n有____个.
(3)观察表格中的数据,请写出一条你发现的结论.
|x|17|17.1|17.2|17.3|17.4|17.5|
|$x^2$|289|292.41|295.84|299.29|302.76|306.25|
|x|17.6|17.7|17.8|17.9|18|
|$x^2$|309.76|313.29|316.84|320.41|324|

(1)316.84的平方根是____;$\sqrt{299.3}\approx$____;$\sqrt{29241}= $____.
(2)若$\sqrt{n}$介于17.6与17.7之间,则满足条件的整数n有____个.
(3)观察表格中的数据,请写出一条你发现的结论.
答案:
(1)±17.8 17.3 171 【解析】
∵ $(\pm17.8)^2=316.84$,
∴ 316.84 的平方根是±17.8.
∵ $17.3^2≈299.3$,
∴ $\sqrt{299.3}≈17.3$.
∵ $171^2=29241$,
∴ $\sqrt{29241}=171$. 故答案为±17.8,17.3,171.
(2)4 【解析】
∵ $\sqrt{309.76}=17.6$,$\sqrt{313.29}=17.7$,且$\sqrt{n}$介于 17.6 与 17.7 之间,
∴ 整数 n 的值可能为 310,311,312,313,
∴ 满足条件的整数 n 有 4 个. 故答案为 4.
(3)【解】发现的结论:当 x>0 时,随着 x 的增大,$x^2$也增大.(答案不唯一)
(1)±17.8 17.3 171 【解析】
∵ $(\pm17.8)^2=316.84$,
∴ 316.84 的平方根是±17.8.
∵ $17.3^2≈299.3$,
∴ $\sqrt{299.3}≈17.3$.
∵ $171^2=29241$,
∴ $\sqrt{29241}=171$. 故答案为±17.8,17.3,171.
(2)4 【解析】
∵ $\sqrt{309.76}=17.6$,$\sqrt{313.29}=17.7$,且$\sqrt{n}$介于 17.6 与 17.7 之间,
∴ 整数 n 的值可能为 310,311,312,313,
∴ 满足条件的整数 n 有 4 个. 故答案为 4.
(3)【解】发现的结论:当 x>0 时,随着 x 的增大,$x^2$也增大.(答案不唯一)
查看更多完整答案,请扫码查看


