《2025年初中必刷题八年级数学上册华师大版》

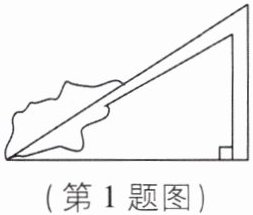
1 [2025河南濮阳期中]如图，在一块平地上，张大爷家前9m处有一棵大树，在一次强风中，这棵大树离地面6m处折断向张大爷家的方向倒下，量得倒下部分的长是10m，大树倒下时会砸到张大爷家吗( )

A.一定不会
B.可能会
C.一定会
D.以上答案都不对

答案：
A 【解析】如图，由勾股定理得，BC = $\sqrt{AB² - AC²}$ = $\sqrt{10² - 6²}$ = 8(m). 因为8 ＜ 9，所以大树倒下时不会砸到张大爷家. 故选A.

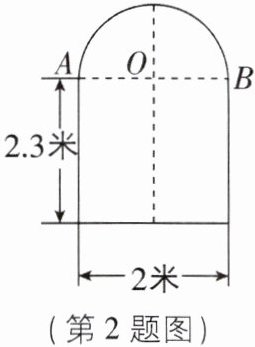
2 一辆装满货物，宽为1.6米的卡车，欲通过如图所示的隧道，则卡车的高必须低于( )

A.3.0米
B.2.9米
C.2.8米
D.2.7米

答案：
B 【解析】
∵卡车宽为1.6米，
∴欲通过题图所示的隧道，只要卡车的高比距隧道中线0.8米处隧道的高度低即可，如图. 在Rt△OCD中，由勾股定理可得CD = $\sqrt{OC² - OD²}$ = $\sqrt{1² - (0.8)²}$ = 0.6(米)，
∴CH = CD + DH = 0.6 + 2.3 = 2.9(米)，
∴卡车的高必须低于2.9米. 故选B.

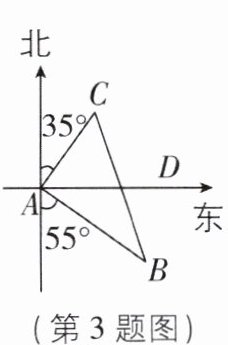
3 [2025河南周口期中]如图，甲、乙两船同时从港口A出发，甲船以30海里/时的速度沿北偏东35°方向航行，乙船沿南偏东55°方向航行，2小时后，甲船到达C岛，乙船到达B岛，若C，B两岛相距100海里，则乙船的速度是______海里/时.

答案：
40 【解析】如图，
∵甲船的速度是30海里/时，航行了2小时，
∴AC = 60海里.
∵∠EAC = 35°，∠FAB = 55°，
∴∠CAB = 90°.
∵BC = 100海里，
∴AB = $\sqrt{BC² - AC²}$ = $\sqrt{100² - 60²}$ = 80(海里)，
∴乙船的速度是40海里/时，故答案为40.

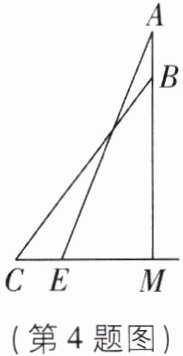
4 “冰雪同梦，亚洲同心”，第九届亚洲冬季运动会于2025年2月7日至2月14日在哈尔滨举办.如图，某校做了一张亚冬会宣传海报(AB)，悬挂在体育馆的上方.小明搬来一架5米长的梯子，顶端靠在宣传海报(AB)的A处，底端落在水平地面上的E处，然后移动梯子使顶端落在宣传海报(AB)的B处，而底端向外移动了1米落在C处(CE=1米).测量得宣传海报(AB)的B处距水平地面4米，即BM=4米，则宣传海报(AB)的长度为______.

答案： ( $\sqrt{21}$ - 4)米 【解析】由题意可得，AE = BC = 5米，BM = 4米，EC = 1米. 在Rt△MBC中，MC = $\sqrt{BC² - BM²}$ = $\sqrt{5² - 4²}$ = 3(米)，则EM = 3 - 1 = 2(米). 在Rt△AEM中，AM = $\sqrt{AE² - EM²}$ = $\sqrt{5² - 2²}$ = $\sqrt{21}$(米)，故AB = AM - BM = ( $\sqrt{21}$ - 4)米.

5 [2024重庆南岸区期末]如图，一个长方体盒子，其中AB=9，BC=3，M为AB上靠近A的三等分点，在大长方体盒子上有一个小长方体盒子，EC=6，CG=1，CF=4.一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N，那么它爬行的最短路程为______.

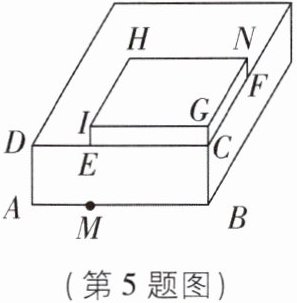
答案：
10 【解析】如图，将面ABCD，CEIG，HIGN展开在同一个平面内，连结MN，则MN为最短路径. 由题意知BM = 6，GN = 4，∠B = 90°，
∴BN = BC + CG + GN = 8. 由勾股定理得MN = $\sqrt{BM² + BN²}$ = 10，故答案为10.

6 [2025山东青岛期中]如图，四边形ABCD中，AB=15m，CD=8m，AD=17m，AE⊥BC于E，且E恰好是BC的中点，AE=12m，则四边形ABCD的面积为______m².

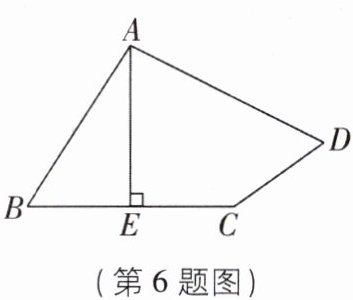
答案： 168 【解析】连结AC.
∵AE⊥BC于E，
∴∠AEB = 90°. 在Rt△ABE中，
∵AB = 15m，AE = 12m，
∴BE = $\sqrt{AB² - AE²}$ = $\sqrt{15² - 12²}$ = 9(m).
∵E是BC的中点，
∴BC = 2BE = 18m，
∴S△ABC = $\frac{1}{2}$BC·AE = $\frac{1}{2}$×18×12 = 108(m²).
∵AE⊥BC，E是BC的中点，
∴AC = AB = 15m.
∵AD = 17m，CD = 8m，
∴CD² + AC² = AD²，
∴∠ACD = 90°，
∴S△ADC = $\frac{1}{2}$AC·CD = $\frac{1}{2}$×15×8 = 60(m²)，
∴S四边形ABCD = S△ABC + S△ADC = 108 + 60 = 168(m²).

7 [2025安徽合肥期中]如图(1)是小聪同学在正方形网格中(每个小正方形的边长为1)画出的格点△ABC(△ABC的三个顶点都在正方形的顶点处)，易知AB=√{5}，BC=√{10}，AC=√{13}.
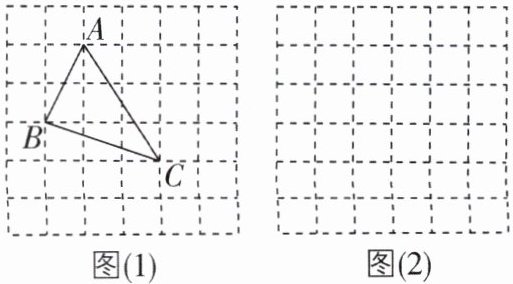
(1)请你参照小聪的方法在图(2)的正方形网格中画出格点△DEF，使得DE=√{2}，EF=√{8}，DF=√{10}；
(2)判断△DEF的形状，并说明理由.

答案：
【解】
(1)如下图，△DEF即为所求.

(2)△DEF为直角三角形. 理由：
∵DE² + EF² = ( $\sqrt{2}$)² + ( $\sqrt{8}$)² = 10，DF² = ( $\sqrt{10}$)² = 10，
∴DE² + EF² = DF²，
∴△DEF为直角三角形.