《2025年初中必刷题八年级数学上册华师大版》

1[2023浙江台州中考]如图,锐角三角形ABC中,AB= AC,点D,E分别在边AB,AC上,连结BE,CD。下列命题中,假命题是( )


A.若CD= BE,则∠DCB= ∠EBC
B.若∠DCB= ∠EBC,则CD= BE
C.若BD= CE,则∠DCB= ∠EBC
D.若∠DCB= ∠EBC,则BD= CE

答案： A 【解析】
∵ AB=AC，
∴ ∠ABC=∠ACB.
∵ CD=BE，BC=CB，
∴ △BCD 与△CBE 满足两边及其中一边的对角分别相等，无法证明全等，因此无法得出∠DCB=∠EBC，故 A 是假命题；若∠DCB=∠EBC，则∠ACD=∠ABE. 在△ABE 和△ACD 中，{∠ABE=∠ACD,AB=AC,∠A=∠A,
∴ △ABE≌△ACD（ASA），
∴ CD=BE，故 B 是真命题；若 BD=CE，则AD=AE. 在△ABE 和△ACD 中，{AB=AC,∠A=∠A,AE=AD,
∴ △ABE≌△ACD（SAS），
∴ ∠ACD=∠ABE.
∵ ∠ABC=∠ACB，
∴ ∠DCB=∠EBC，故 C 是真命题；若∠DCB=∠EBC，则在△DBC 和△ECB 中，{∠ABC=∠ACB,BC=BC,∠DCB=∠EBC,
∴ △DBC≌△ECB（ASA），
∴ BD=CE，故 D 是真命题. 故选 A.

2[2024江苏无锡中考]命题“若a＞b,则a-3＜b-3”是______命题。(填“真”或“假”)

答案： 假 【解析】
∵ a＞b，
∴ a-3＞b-3，
∴ 命题"若a＞b，则a-3＜b-3"是假命题，故答案为假.

3[2023吉林长春中考改编]如图,工人师傅设计了一种测零件内径AB的卡钳,卡钳交叉点O为AA',BB'的中点,只要量出A'B'的长度,就可以知道该零件内径AB的长度。依据的数学基本事实是( )


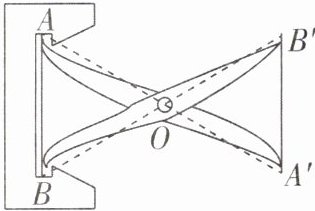
A.两边及其夹角分别相等的两个三角形全等
B.两角及其夹边分别相等的两个三角形全等
C.两角及其中一角的对边分别相等的两个三角形全等
D.两点之间线段最短

答案： A 【解析】
∵ O 为 AA'，BB'的中点，
∴ OA=OA'，OB=OB'.
∵ ∠AOB=∠A'OB'（对顶角相等），
∴ 在△AOB 与△A'OB'中，{OA=OA',∠AOB=∠A'OB',OB=OB',
∴ △AOB≌△A'OB'（SAS），
∴ AB=A'B'，故选 A.

4[2023重庆中考A卷]如图,在Rt△ABC中,∠BAC= 90°,AB= AC,点D为BC上一点,连结AD。过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F。若BE= 4,CF= 1,则EF的长度为______。

答案： 3 【解析】
∵ ∠BAC=90°，
∴ ∠EAB+∠EAC=90°.
∵ BE⊥AD，CF⊥AD，
∴ ∠AEB=∠AFC=90°，
∴ ∠ACF+∠EAC=90°，
∴ ∠ACF=∠BAE.在△AFC 和△BEA 中，{∠CFA=∠AEB,∠ACF=∠BAE,AC=AB,
∴ △AFC≌△BEA（AAS），
∴ AF=BE=4，AE=CF=1，
∴ EF=AF-AE=4-1=3，故答案为 3.

5新考法[2024四川遂宁中考]在等边△ABC三边上分别取点D,E,F,使得AD= BE= CF,连结三点得到△DEF,易得△ADF≌△BED≌△CFE,设S_△ABC= 1,则S_△DEF= 1-3S_△ADF。

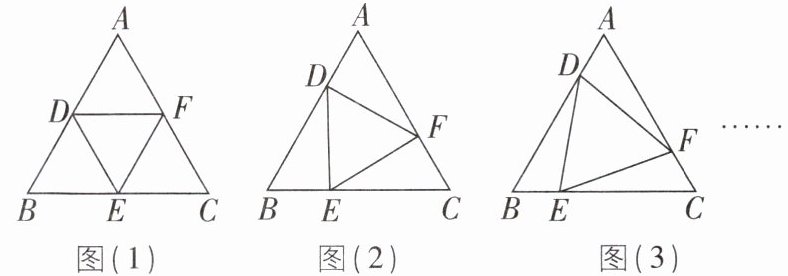
如图(1),当AD/AB= 1/2时,S_△DEF= 1-3×1/4= 1/4；
如图(2),当AD/AB= 1/3时,S_△DEF= 1-3×2/9= 1/3；
如图(3),当AD/AB= 1/4时,S_△DEF= 1-3×3/16= 7/16；
……
直接写出,当AD/AB= 1/10时,S_△DEF= ______。

答案： 73/100 【解析】当AD/AB=1/2时，S△DEF=1-3×(2-1)/2²=1/4；当AD/AB=1/3时，S△DEF=1-3×(3-1)/3²=1/3；当AD/AB=1/4时，S△DEF=1-3×(4-1)/4²=7/16；…；当AD/AB=1/n（n≥2且n为整数）时，S△DEF=1-3×(n-1)/n²，故当AD/AB=1/10时，S△DEF=1-3×(10-1)/10²=73/100.

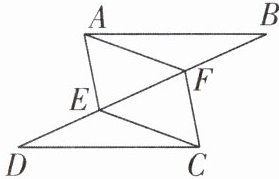
6新考向开放性试题[2024山东淄博中考]如图,已知AB= CD,点E,F在线段BD上,且AF= CE。请从①BF= DE,②∠BAF= ∠DCE,③AF= CF中,选择一个合适的选项作为已知条件,使得△ABF≌△CDE。
你添加的条件是______(只填写一个序号)。
添加条件后,请证明AE//CF。

答案： 【解】选择①BF=DE时，△ABF≌△CDE，证明如下：在△ABF 和△CDE 中，{AB=CD,AF=CE,BF=DE,
∴ △ABF≌△CDE（SSS），
∴ ∠B=∠D.
∵ BF=DE，
∴ BF+EF=DE+EF，即 BE=DF. 在△ABE和△CDF 中，{AB=CD,∠B=∠D,BE=DF,
∴ △ABE≌△CDF（SAS），
∴ ∠AEB=∠CFD，
∴ AE//CF. 选择②∠BAF=∠DCE时，△ABF≌△CDE，证明如下：在△ABF 和△CDE 中，{AB=CD,∠BAF=∠DCE,AF=CE,
∴ △ABF≌△CDE（SAS），
∴ ∠B=∠D，BF=DE，同理可证△ABE≌△CDF（SAS），
∴ ∠AEB=∠CFD，
∴ AE//CF. 选择③AF=CF时，不能判定△ABF≌△CDE. 故答案为①（或②）（根据添加的条件证明即可）.

7[2024四川南充中考]如图,在△ABC中,点D为BC边的中点,过点B作BE//AC交AD的延长线于点E。
(1)求证：△BDE≌△CDA。
(2)若AD⊥BC,求证：BA= BE。

答案： 【证明】（1）
∵ 点 D 为 BC 边的中点，
∴ BD=CD.
∵ BE//AC，
∴ ∠EBD=∠C，∠E=∠CAD.在△BDE 和△CDA 中，{∠EBD=∠C,∠E=∠CAD,BD=CD,
∴ △BDE≌△CDA（AAS）.（2）
∵ △BDE≌△CDA，
∴ ED=AD.
∵ AD⊥BC，
∴ BD 垂直平分 AE，
∴ BA=BE.