第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1[2025河南郑州期末,中]在△ABC中,∠B=∠C=50°,将△ABC沿图中虚线剪开,剪下的两个三角形不一定全等的是( )
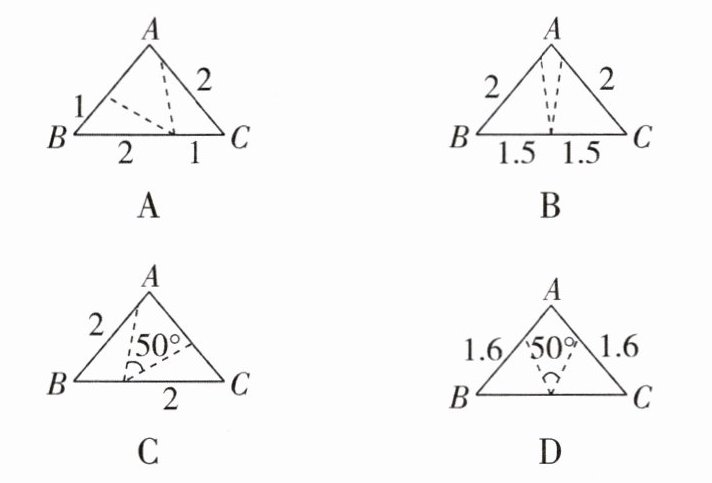
A.
B.
C.
D.

A.
B.
C.
D.
答案:
1.D [解析]A选项,根据SAS可以推出剪下的两个三角形全等,故A选项不符合题意.B选项,根据SAS可以推出剪下的两个三角形全等,故B选项不符合题意.C选项,如图
(1),
∵∠DFC=∠DFE+∠EFC=∠B+∠BDF,∠B=∠DFE=50°,
∴∠EFC=∠BDF.
∵BD=FC,∠B=∠C,
∴△DBF≌△FCE(ASA),故C选项不符合题意.D选项,如图
(2),同C选项可得∠EFC=∠BDF,而∠B=∠C,BD=CE,相等的边并不都是两组相等角的夹边,
∴两个三角形不一定全等,故D选项符合题意.故选D.


1.D [解析]A选项,根据SAS可以推出剪下的两个三角形全等,故A选项不符合题意.B选项,根据SAS可以推出剪下的两个三角形全等,故B选项不符合题意.C选项,如图
(1),
∵∠DFC=∠DFE+∠EFC=∠B+∠BDF,∠B=∠DFE=50°,
∴∠EFC=∠BDF.
∵BD=FC,∠B=∠C,
∴△DBF≌△FCE(ASA),故C选项不符合题意.D选项,如图
(2),同C选项可得∠EFC=∠BDF,而∠B=∠C,BD=CE,相等的边并不都是两组相等角的夹边,
∴两个三角形不一定全等,故D选项符合题意.故选D.


2[2025陕西咸阳质检,中]如图,在四边形ABCD中,AD//BC,∠C=90°,∠ABC和∠BAD的平分线交于点P,点P在CD上,PE⊥AB于点E. 若四边形ABCD的面积为78,AB=13,则CD的长为( )
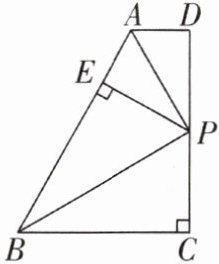
A.6
B.10
C.12
D.18

A.6
B.10
C.12
D.18
答案:
2.C [解析]
∵AD//BC,∠C=90°,
∴∠D=90°.
∵PE⊥AB于点E,
∴∠PEA=∠PEB=90°.
∵AP平分∠BAD,BP平分∠ABC,
∴∠DAP=∠EAP,∠EBP=∠CBP.在△DAP与△EAP中,∠D=∠AEP=90°,∠DAP=∠EAP,AP=AP,
∴△DAP≌△EAP(AAS),同理可得△EBP≌△CBP(AAS),
∴AD=AE,BE=BC,
∴S梯形ABCD=$\frac{1}{2}$(AD+BC)·DC=$\frac{1}{2}$(AE+BE)·DC=$\frac{1}{2}$AB·DC=78.
∵AB=13,
∴DC=12.故选C.
∵AD//BC,∠C=90°,
∴∠D=90°.
∵PE⊥AB于点E,
∴∠PEA=∠PEB=90°.
∵AP平分∠BAD,BP平分∠ABC,
∴∠DAP=∠EAP,∠EBP=∠CBP.在△DAP与△EAP中,∠D=∠AEP=90°,∠DAP=∠EAP,AP=AP,
∴△DAP≌△EAP(AAS),同理可得△EBP≌△CBP(AAS),
∴AD=AE,BE=BC,
∴S梯形ABCD=$\frac{1}{2}$(AD+BC)·DC=$\frac{1}{2}$(AE+BE)·DC=$\frac{1}{2}$AB·DC=78.
∵AB=13,
∴DC=12.故选C.
3新考法[2025江苏南京期中,中]如图,在同一平面内,直线l同侧有三个正方形A,B,C,若正方形A,C的面积分别为25和9,则阴影部分的总面积为______.


答案:
3.15 [解析]如图,作PD⊥PG,NE⊥NK,QE⊥NE于E,PD与QE交于点D,则易知PD⊥QE.
∵正方形A,C的面积分别为25和9,
∴PG=5,NK=3.
∵A,B,C为正方形,
∴PQ=PF,∠QPF=90°,∠PDQ=∠PGF=90°,
∴∠GPF+∠DPF=∠DPF+∠DPQ=90°,
∴∠GPF=∠DPQ,
∴△GPF≌△DPQ(AAS),
∴DQ=GF,PD=PG=5.同理可得GF=NK=3,PG=FK=5,EN=NK=3,QE=FK=5,
∴DQ=3,
∴S阴影部分=$\frac{1}{2}$×5×3+$\frac{1}{2}$×3×5=15.故答案为15.

3.15 [解析]如图,作PD⊥PG,NE⊥NK,QE⊥NE于E,PD与QE交于点D,则易知PD⊥QE.
∵正方形A,C的面积分别为25和9,
∴PG=5,NK=3.
∵A,B,C为正方形,
∴PQ=PF,∠QPF=90°,∠PDQ=∠PGF=90°,
∴∠GPF+∠DPF=∠DPF+∠DPQ=90°,
∴∠GPF=∠DPQ,
∴△GPF≌△DPQ(AAS),
∴DQ=GF,PD=PG=5.同理可得GF=NK=3,PG=FK=5,EN=NK=3,QE=FK=5,
∴DQ=3,
∴S阴影部分=$\frac{1}{2}$×5×3+$\frac{1}{2}$×3×5=15.故答案为15.

4[较难]如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高,点E从点B出发,在直线BC上以2cm/s的速度运动,过点E作BC的垂线交直线CD于点F,当点E运动______s时,CF=AB.
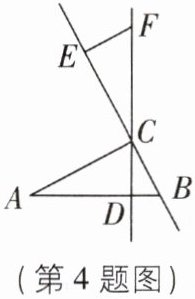

答案:
4.2或5 [解析]
∵∠ACB=90°,
∴∠A+∠CBD=90°.
∵CD为AB边上的高,
∴∠CDB=90°,
∴∠BCD+∠CBD=90°,
∴∠A=∠BCD.
∵∠BCD=∠ECF,
∴∠ECF=∠A.
∵过点E作BC的垂线交直线CD于点F,
∴∠CEF=90°=∠ACB.在△CEF和△ACB中,∠ECF=∠A,∠CEF=∠ACB,CF=AB,
∴△CEF≌△ACB(AAS),
∴CE=AC=7cm.①如图,当点E在射线BC上移动时,BE=CE+BC=7+3=10(cm).
∵点E从点B出发,在直线BC上以2cm/s的速度运动,
∴点E运动了$\frac{10}{2}$=5(s).②当点E在射线CB上运动时,BE'=AC−BC=7−3=4(cm).
∵点E从点B出发,在直线BC上以2cm/s的速度运动,
∴点E运动了$\frac{4}{2}$=2(s).综上所述,当点E运动5s或2s时,CF=AB.故答案为2或5.
思路分析:先证明△DAP≌△EAP,△EBP≌△CBP,得到AD=AE,BE=BC,再根据S梯形ABCD=$\frac{1}{2}$(AD+BC)·DC=$\frac{1}{2}$(AE+BE)·DC=$\frac{1}{2}$AB·DC求解即可.
关键点拔:
(2)根据ASA证出△AEB≌△CEB,可得AE=CE,即可求解.
思路分析:先证明△CEF≌△ACB(AAS),得出CE=AC=7cm,再分情况讨论:①当点E在射线BC上运动时,BE=CE+BC=10cm,即可求出点E运动了5s;②当点E在射线CB上运动时,BE'=AC - BC=4cm,即可求出点E运动了2s.

4.2或5 [解析]
∵∠ACB=90°,
∴∠A+∠CBD=90°.
∵CD为AB边上的高,
∴∠CDB=90°,
∴∠BCD+∠CBD=90°,
∴∠A=∠BCD.
∵∠BCD=∠ECF,
∴∠ECF=∠A.
∵过点E作BC的垂线交直线CD于点F,
∴∠CEF=90°=∠ACB.在△CEF和△ACB中,∠ECF=∠A,∠CEF=∠ACB,CF=AB,
∴△CEF≌△ACB(AAS),
∴CE=AC=7cm.①如图,当点E在射线BC上移动时,BE=CE+BC=7+3=10(cm).
∵点E从点B出发,在直线BC上以2cm/s的速度运动,
∴点E运动了$\frac{10}{2}$=5(s).②当点E在射线CB上运动时,BE'=AC−BC=7−3=4(cm).
∵点E从点B出发,在直线BC上以2cm/s的速度运动,
∴点E运动了$\frac{4}{2}$=2(s).综上所述,当点E运动5s或2s时,CF=AB.故答案为2或5.
思路分析:先证明△DAP≌△EAP,△EBP≌△CBP,得到AD=AE,BE=BC,再根据S梯形ABCD=$\frac{1}{2}$(AD+BC)·DC=$\frac{1}{2}$(AE+BE)·DC=$\frac{1}{2}$AB·DC求解即可.
关键点拔:
(2)根据ASA证出△AEB≌△CEB,可得AE=CE,即可求解.
思路分析:先证明△CEF≌△ACB(AAS),得出CE=AC=7cm,再分情况讨论:①当点E在射线BC上运动时,BE=CE+BC=10cm,即可求出点E运动了5s;②当点E在射线CB上运动时,BE'=AC - BC=4cm,即可求出点E运动了2s.

5[中]如图,在△ABC中,AB=BC,∠ABC=45°,CD⊥AB于点D,BE⊥AC于点E,且BE,CD相交于点F.
(1)求证:△BDF≌△CDA;
(2)若BE平分∠ABC,BF=10,求CE的长.
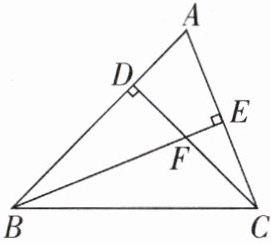
(1)求证:△BDF≌△CDA;
(2)若BE平分∠ABC,BF=10,求CE的长.

答案:
5.
(1)[证明]
∵CD⊥AB,BE⊥AC,
∴∠BDF=∠ADC=∠FEC=90°.
∵∠BDF=90°,∠ABC=45°,
∴∠BCD=45°,
∴△BDC是等腰直角三角形,
∴BD=CD.
∵∠DBF=90°−∠BFD,∠DCA=90°−∠EFC,且∠BFD=∠EFC,
∴∠DBF=∠DCA.在△BDF和△CDA中,∠BDF=∠ADC,BD=CD,∠DBF=∠ACD,
∴△BDF≌△CDA(ASA).
(2)[解]
∵BE平分∠ABC,
∴∠ABE=∠CBE.在△BEA和△BEC中,∠AEB=∠CEB,BE=BE,∠ABE=∠CBE,
∴△BEA≌△BEC(ASA),
∴AE=CE=$\frac{1}{2}$AC.
∵△BDF≌△CDA,
∴AC=BF,
∴CE=$\frac{1}{2}$AC=$\frac{1}{2}$BF=5.
(1)[证明]
∵CD⊥AB,BE⊥AC,
∴∠BDF=∠ADC=∠FEC=90°.
∵∠BDF=90°,∠ABC=45°,
∴∠BCD=45°,
∴△BDC是等腰直角三角形,
∴BD=CD.
∵∠DBF=90°−∠BFD,∠DCA=90°−∠EFC,且∠BFD=∠EFC,
∴∠DBF=∠DCA.在△BDF和△CDA中,∠BDF=∠ADC,BD=CD,∠DBF=∠ACD,
∴△BDF≌△CDA(ASA).
(2)[解]
∵BE平分∠ABC,
∴∠ABE=∠CBE.在△BEA和△BEC中,∠AEB=∠CEB,BE=BE,∠ABE=∠CBE,
∴△BEA≌△BEC(ASA),
∴AE=CE=$\frac{1}{2}$AC.
∵△BDF≌△CDA,
∴AC=BF,
∴CE=$\frac{1}{2}$AC=$\frac{1}{2}$BF=5.
6核心素养推理能力[较难]问题情境:如图(1),∠AOB=90°,OC平分∠AOB,三角尺的直角顶点落在OC的任意一点P上,并使三角尺的两条直角边分别与OA,OB相交于点E,F,PE与PF相等吗?请你给出证明;
变式拓展:如图(2),已知∠AOB=120°,OC平分∠AOB,P是OC上一点,∠EPF=60°,PE与OA相交于点E,PF与射线OB的反向延长线相交于点F. PE与PF相等吗?请说明理由.

变式拓展:如图(2),已知∠AOB=120°,OC平分∠AOB,P是OC上一点,∠EPF=60°,PE与OA相交于点E,PF与射线OB的反向延长线相交于点F. PE与PF相等吗?请说明理由.

答案:
6.[解]问题情境:PE=PF.证明:如图
(1),过点P作PM⊥OB于M,PN⊥OA于N.
∵OC平分∠AOB,
∴∠PON=∠POM.在△PNO和△PMO中,∠PNO=∠PMO,∠PON=∠POM,PO=PO,
∴△PNO≌△PMO(AAS),
∴PN=PM.
∵∠PMO=∠PNO=∠MON=90°,
∴∠MPN=360°−3×90°=90°.
∵∠MPN=∠EPF=90°,
∴∠MPF=∠NPE.在△PMF和△PNE中,∠MPF=∠NPE,PM=PN,∠PMF=∠PNE=90°,
∴△PMF≌△PNE(ASA),
∴PF=PE.

变式拓展:PE=PF.理由:如图
(2),过点P作PM⊥OB于M,PN⊥OA于N.
∵OC平分∠AOB,
∴∠POM=∠PON.在△POM和△PON中,∠PMO=∠PNO,∠POM=∠PON,PO=PO,
∴△POM≌△PON(AAS),
∴PM=PN.
∵∠MON=120°,
∴∠MPN=360°−2×90°−120°=60°.
∵∠MPN=∠EPF=60°,
∴∠MPF=∠NPE.在△PMF和△PNE中,∠MPF=∠NPE,PM=PN,∠PMF=∠PNE=90°,
∴△PMF≌△PNE(ASA),
∴PF=PE.

6.[解]问题情境:PE=PF.证明:如图
(1),过点P作PM⊥OB于M,PN⊥OA于N.
∵OC平分∠AOB,
∴∠PON=∠POM.在△PNO和△PMO中,∠PNO=∠PMO,∠PON=∠POM,PO=PO,
∴△PNO≌△PMO(AAS),
∴PN=PM.
∵∠PMO=∠PNO=∠MON=90°,
∴∠MPN=360°−3×90°=90°.
∵∠MPN=∠EPF=90°,
∴∠MPF=∠NPE.在△PMF和△PNE中,∠MPF=∠NPE,PM=PN,∠PMF=∠PNE=90°,
∴△PMF≌△PNE(ASA),
∴PF=PE.

变式拓展:PE=PF.理由:如图
(2),过点P作PM⊥OB于M,PN⊥OA于N.
∵OC平分∠AOB,
∴∠POM=∠PON.在△POM和△PON中,∠PMO=∠PNO,∠POM=∠PON,PO=PO,
∴△POM≌△PON(AAS),
∴PM=PN.
∵∠MON=120°,
∴∠MPN=360°−2×90°−120°=60°.
∵∠MPN=∠EPF=60°,
∴∠MPF=∠NPE.在△PMF和△PNE中,∠MPF=∠NPE,PM=PN,∠PMF=∠PNE=90°,
∴△PMF≌△PNE(ASA),
∴PF=PE.

查看更多完整答案,请扫码查看


