《2025年初中必刷题八年级数学上册华师大版》

1 [2025 河北沧州质检,中]若 $\underbrace{2^{3}+2^{3}+2^{3}+… +2^{3}}_{k个2^{3}}= 2^{m}(k\gt 1,k,m$ 都为正整数),则 $m$ 的最小值为( )

A.3
B.4
C.6
D.9

答案： B【解析】$\because \underbrace{2^{3}+2^{3}+2^{3}+\cdots +2^{3}}_{k个2^{3}}=2^{m}$（$k＞1$，$k,m$都为正整数）,$\therefore 2^{3}k=2^{m}$，则$k$是可以转化为以$2$为底数幂的形式的数，$\therefore k$的最小值为$2=2^{1}$，$\therefore 2^{3}× 2=2^{m}$，$\therefore m=4$，$\therefore m$的最小值为 4.故选 B.

2 新考法 [2025 吉林长春期中,中]我们知道,同底数幂的乘法法则为 $a^{m}\cdot a^{n}= a^{m + n}$(其中 $a\neq 0$, $m$, $n$ 为正整数),类似地,我们规定关于任意正整数 $m$, $n$ 的一种新运算: $h(m + n)= h(m)\cdot h(n)$.比如 $h(2)= 3$,则 $h(4)= h(2 + 2)= h(2)\cdot h(2)= 3× 3 = 9$.若 $h(2)= k$,则 $h(2n)\cdot h(2020)$ 的结果是( )

A.$2k + 2021$
B.$k^{n + 2020}$
C.$k^{n + 1012}$
D.$k^{n + 1010}$

答案： D【解析】$h(4)=h(2+2)=k× k=k^{2}$，$h(6)=h(4+2)=h(4)\cdot h(2)=k^{3}$，$h(8)=h(6+2)=h(6)\cdot h(2)=k^{4}$，$\cdots$，$\therefore h(2n)=k^{n}$，则$h(2020)=h(2× 1010)=k^{1010}$，$\therefore h(2n)\cdot h(2020)=k^{n}\cdot k^{1010}=k^{n+1010}$，故选 D.

3 [2025 河南周口期中]电子文件的大小常用 B, KB, MB, GB 等作为单位,其中 $1\mathrm{GB}= 2^{10}\mathrm{MB}$, $1\mathrm{MB}= 2^{10}\mathrm{KB}$, $1\mathrm{KB}= 2^{10}\mathrm{B}$.若某视频文件的大小约为 $2\mathrm{GB}$,则 $2\mathrm{GB}= $______$\mathrm{B}$.

答案： $2^{31}$【解析】根据题意，得$2\ \text{GB}=2× 2^{10}× 2^{10}× 2^{10}\ \text{B}=2^{31}\ \text{B}$ ,故答案为$2^{31}$.

4 [中]若 $m = 3^{a}$, $3m = 3^{b}$,则 $b= $______.(用含 $a$ 的式子表示)

答案： $a+1$【解析】$\because m=3^{a}$，$\therefore 3m=3× 3^{a}=3^{a+1}=3^{b}$，$\therefore b=a+1$. 故答案为$a+1$.

5 [2024 安徽安庆期末,中]已知按一定规律排列的一列数: $a$, $a^{2}$, $a^{3}$, $a^{5}$, $a^{8}$, $a^{13}$, …$(a\gt 0)$.若 $x$, $y$, $z(x\lt y\lt z)$ 表示这列数中的连续三个数,猜想 $x$, $y$, $z$ 满足的关系式是______。

答案： $xy=z$【解析】$\because a^{1}× a^{2}=a^{3}$,$a^{2}× a^{3}=a^{5}$,$a^{3}× a^{5}=a^{8}$,$a^{5}× a^{8}=a^{13}$,$\cdots$,$\therefore x,y,z$满足的关系式是$xy=z$. 故答案为$xy=z$.

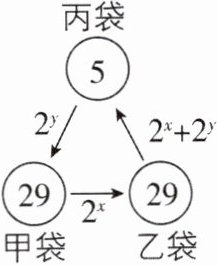
6 新考法 [2025 河北石家庄期中,中]如图,在甲、乙、丙三只袋中分别装有球 29 个、29 个、5 个.先从甲袋中取出 $2^{x}$ 个球放入乙袋,再从乙袋中取出 $(2^{x}+2^{y})$ 个球放入丙袋,最后从丙袋中取出 $2^{y}$ 个球放入甲袋,此时三只袋中球的个数相同,则 $2^{x + y}$ 的值等于______。

答案： 128【解析】由题意可知,调整后三只袋中球的个数为甲袋:$(29-2^{x}+2^{y})$个,乙袋:$29+2^{x}-(2^{x}+2^{y})=(29-2^{y})$个,丙袋:$5+(2^{x}+2^{y})-2^{y}=(5+2^{x})$个.$\because$一共有$29 + 29+5=63$(个)球,且调整后三只袋中球的个数相同,$\therefore$调整后每只袋中球的个数为$63÷ 3=21$(个),$\therefore 5+2^{x}=21$,$29-2^{y}=21$,$\therefore 2^{x}=16$,$2^{y}=8$,$\therefore 2^{x+y}=2^{x}\cdot 2^{y}=16× 8=128$,故答案为$128$.

7 [中]已知 $10^{\alpha}=3$, $10^{\beta}=5$, $10^{\gamma}=7$,试把 105 写成底数是 10 的幂的形式:______。

答案： $10^{\alpha+\beta+\gamma}$【解析】$\because 105=3× 5× 7$,$3=10^{\alpha}$,$5=10^{\beta}$,$7=10^{\gamma}$,$\therefore 105=10^{\alpha}\cdot 10^{\beta}\cdot 10^{\gamma}=10^{\alpha+\beta+\gamma}$.故答案为$10^{\alpha+\beta+\gamma}$.

8 [中]已知 $x = 2^{m}+1$, $y = 3 + 2^{m + 1}$,若用含 $x$ 的代数式表示 $y$,则 $y= $______。

答案： $2x + 1$【解析】$\because x=2^{m}+1$,$\therefore 2^{m}=x - 1$.$\because 2^{m+1}=2\cdot 2^{m}$,$\therefore 2^{m+1}=2(x - 1)$,$\therefore y=3+2^{m+1}=3 + 2(x - 1)=2x + 1$.故答案为$2x + 1$.

9 [2025 四川自贡期中,中]
(1)已知 $a^{x}= 5$, $a^{x + y}= 25$,求 $a^{x}+a^{y}$ 的值.
(2)已知 $x^{2a + b}\cdot x^{3a - b}\cdot x^{a}= x^{12}$,求 $-a^{100}+2^{101}$ 的值.

答案： （1）$\because a^{x}=5$,$\therefore a^{x + y}=a^{x}\cdot a^{y}=5a^{y}=25$,$\therefore a^{y}=5$,$\therefore a^{x}+a^{y}=5 + 5=10$.
(2)$\because x^{2a + b}\cdot x^{3a - b}\cdot x^{a}=x^{12}$,$\therefore x^{6a}=x^{12}$,$\therefore 6a=12$,$\therefore a=2$,$\therefore -a^{100}+2^{101}=-2^{100}+2^{101}=-2^{100}+2× 2^{100}=2^{100}$.

10 核心素养 运算能力 [较难]阅读材料:求 $1 + 2 + 2^{2}+2^{3}+2^{4}+… +2^{2022}+2^{2023}$ 的值.
解:设 $S = 1 + 2 + 2^{2}+2^{3}+2^{4}+… +2^{2022}+2^{2023}$, ①
将等式两边同时乘 2 得 $2S = 2 + 2^{2}+2^{3}+2^{4}+2^{5}+… +2^{2023}+2^{2024}$, ②
② - ①,得 $2S - S = 2^{2024}-1$,
即 $S = 2^{2024}-1$,
$\therefore 1 + 2 + 2^{2}+2^{3}+2^{4}+… +2^{2022}+2^{2023}= 2^{2024}-1$.
请你仿照此法计算:
(1) $1 + 2 + 2^{2}+2^{3}+2^{4}+… +2^{9}+2^{10}$；
(2) $1 + 3 + 3^{2}+3^{3}+3^{4}+… +3^{n - 1}+3^{n}$(其中 $n$ 为正整数).(结果用含 $n$ 的式子表示)

答案： （1）设$S=1 + 2 + 2^{2}+2^{3}+2^{4}+\cdots +2^{9}+2^{10}$,① 将等式两边同乘2得$2S=2 + 2^{2}+2^{3}+2^{4}+2^{5}+\cdots +2^{10}+2^{11}$,② ②-①,得$S=2^{11}-1$,即$1 + 2 + 2^{2}+2^{3}+2^{4}+\cdots +2^{9}+2^{10}=2^{11}-1$.
(2)设$S=1 + 3 + 3^{2}+3^{3}+3^{4}+\cdots +3^{n - 1}+3^{n}$,① 将等式两边同乘3得$3S=3 + 3^{2}+3^{3}+3^{4}+3^{5}+\cdots +3^{n}+3^{n + 1}$,② ②-①,得$2S=3^{n + 1}-1$,$\therefore S=\frac{1}{2}(3^{n + 1}-1)$,即$1 + 3 + 3^{2}+3^{3}+3^{4}+\cdots +3^{n - 1}+3^{n}=\frac{1}{2}(3^{n + 1}-1)$.