第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2025 四川巴中期中,中]若$(a - b)^2 = 3$,$(a + b)^2 = 7$,则$a^2 + b^2 - 3ab - 2$的值为 ( )
A.0
B.2
C.3
D.4
A.0
B.2
C.3
D.4
答案:
1.A [解析]
∵$(a + b)^{2}-(a - b)^{2}=4ab$,即$4ab = 7 - 3 = 4$,解得$ab = 1$,
∴$a^{2}+b^{2}-3ab - 2=(a - b)^{2}-ab - 2=3 - 1 - 2 = 0$,故选A.
∵$(a + b)^{2}-(a - b)^{2}=4ab$,即$4ab = 7 - 3 = 4$,解得$ab = 1$,
∴$a^{2}+b^{2}-3ab - 2=(a - b)^{2}-ab - 2=3 - 1 - 2 = 0$,故选A.
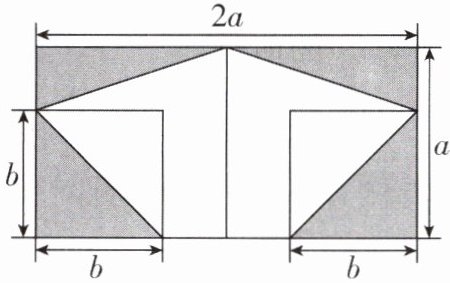
2 [2024 江苏南通海安期末,中]如图,两个大正方形的边长为$a$,两个小正方形的边长为$b$,如果$a - b = 2$,$ab = 26$,那么阴影部分的面积是 ( )
A.30
B.34
C.40
D.44

A.30
B.34
C.40
D.44
答案:
2.A [解析]如图,
∵$a - b = 2$,$ab = 26$,
∴$a^{2}-2ab + b^{2}=4$,
∴$a^{2}+b^{2}=4 + 2ab=4 + 52 = 56$.阴影部分的面积为$S_{\triangle ABC}+S_{\triangle CDM}+S_{\triangle AEF}+S_{\triangle GHM}=2×\frac{1}{2}(a - b)×a+2×\frac{1}{2}b×b=a(a - b)+b^{2}=a^{2}+b^{2}-ab=56 - 26 = 30$.

2.A [解析]如图,
∵$a - b = 2$,$ab = 26$,
∴$a^{2}-2ab + b^{2}=4$,
∴$a^{2}+b^{2}=4 + 2ab=4 + 52 = 56$.阴影部分的面积为$S_{\triangle ABC}+S_{\triangle CDM}+S_{\triangle AEF}+S_{\triangle GHM}=2×\frac{1}{2}(a - b)×a+2×\frac{1}{2}b×b=a(a - b)+b^{2}=a^{2}+b^{2}-ab=56 - 26 = 30$.

3 [2025 浙江金华期末,较难]已知$\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 0$,$a^2 + b^2 + c^2 = 100$,则$a + b + c$的值等于 ( )
A.10
B.-10
C.0
D.10 或 -10
A.10
B.-10
C.0
D.10 或 -10
答案:
3.D [解析]
∵$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0$,
∴$bc + ac + ab = 0$,
∴$2bc + 2ac + 2ab = 0$.
∵$a^{2}+b^{2}+c^{2}=100$,
∴$(a + b + c)^{2}=(a + b)^{2}+2(a + b)c + c^{2}=a^{2}+2ab + b^{2}+2ac + 2bc + c^{2}=a^{2}+b^{2}+c^{2}+2ab + 2ac + 2bc = 100$,
∴$a + b + c = 10$或$-10$.故选D.
∵$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0$,
∴$bc + ac + ab = 0$,
∴$2bc + 2ac + 2ab = 0$.
∵$a^{2}+b^{2}+c^{2}=100$,
∴$(a + b + c)^{2}=(a + b)^{2}+2(a + b)c + c^{2}=a^{2}+2ab + b^{2}+2ac + 2bc + c^{2}=a^{2}+b^{2}+c^{2}+2ab + 2ac + 2bc = 100$,
∴$a + b + c = 10$或$-10$.故选D.
4 [中]计算:$999^2 - 998×1002 = $______。
答案:
4. - 1995 [解析]原式$=(1000 - 1)^{2}-(1000 - 2)×(1000 + 2)=1000^{2}-2×1000×1 + 1^{2}-1000^{2}+2^{2}=-2000 + 1 + 4=-1995$,故答案为 - 1995.
5 [中]设$a = x - 2020$,$b = x - 2022$,$c = x - 2021$。若$a^2 + b^2 = 56$,则$c^2 = $______。
答案:
5.27 [解析]
∵$a = x - 2020$,$b = x - 2022$,$c = x - 2021$,
∴$a = c + 1$,$b = c - 1$.
∵$a^{2}+b^{2}=56$,
∴$(c + 1)^{2}+(c - 1)^{2}=56$,
∴$c^{2}=27$.故答案为27.
∵$a = x - 2020$,$b = x - 2022$,$c = x - 2021$,
∴$a = c + 1$,$b = c - 1$.
∵$a^{2}+b^{2}=56$,
∴$(c + 1)^{2}+(c - 1)^{2}=56$,
∴$c^{2}=27$.故答案为27.
6 <新考向传统文化>[中]我国南宋时期杰出的数学家杨辉是钱塘人,如图是他在《详解九章算法》中记载的“杨辉三角”。此图揭示了$(a + b)^n$($n$为非负整数)的展开式的项数及各项系数的有关规律。
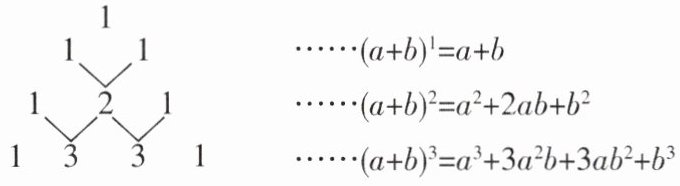
(1) $(a + b)^n$的展开式共有______项,系数和为______。
(2) 根据上面的规律,则$(a - b)^4$的展开式为______。
(3) 利用上面的规律计算:$3^5 - 5×3^4 + 10×3^3 - 10×3^2 + 5×3 - 1$。
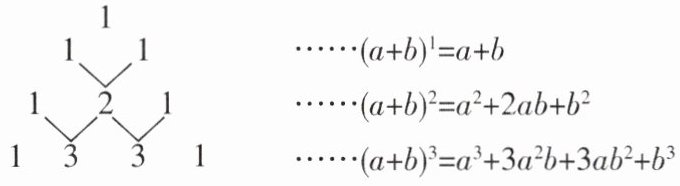
(1) $(a + b)^n$的展开式共有______项,系数和为______。
(2) 根据上面的规律,则$(a - b)^4$的展开式为______。
(3) 利用上面的规律计算:$3^5 - 5×3^4 + 10×3^3 - 10×3^2 + 5×3 - 1$。
答案:
6.[解]
(1)由杨辉三角的系数规律可得$(a + b)^{n}$的展开式共有$(n + 1)$项,系数和为$2^{n}$.故答案为$(n + 1)$,$2^{n}$.
(2)由杨辉三角的系数规律可得$(a - b)^{4}=a^{4}-4a^{3}b + 6a^{2}b^{2}-4ab^{3}+b^{4}$.故答案为$a^{4}-4a^{3}b + 6a^{2}b^{2}-4ab^{3}+b^{4}$.
(3)$3^{5}-5×3^{4}+10×3^{3}-10×3^{2}+5×3 - 1=(3 - 1)^{5}=2^{5}=32$.
(1)由杨辉三角的系数规律可得$(a + b)^{n}$的展开式共有$(n + 1)$项,系数和为$2^{n}$.故答案为$(n + 1)$,$2^{n}$.
(2)由杨辉三角的系数规律可得$(a - b)^{4}=a^{4}-4a^{3}b + 6a^{2}b^{2}-4ab^{3}+b^{4}$.故答案为$a^{4}-4a^{3}b + 6a^{2}b^{2}-4ab^{3}+b^{4}$.
(3)$3^{5}-5×3^{4}+10×3^{3}-10×3^{2}+5×3 - 1=(3 - 1)^{5}=2^{5}=32$.
7 <新考法>[2025 浙江杭州期中,较难]如图(1),正方形 A、B、C 的边长分别为$m$,$n$,$p$。
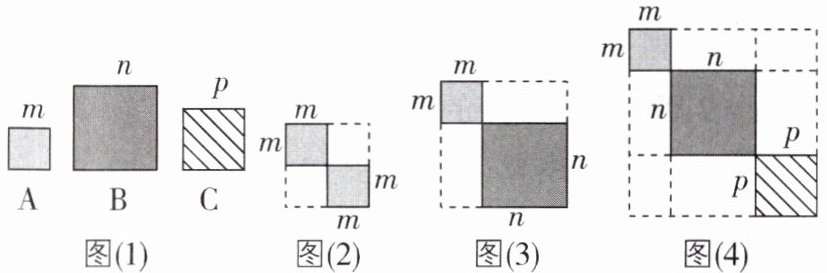
(1) 用两个正方形 A 组合成图(2)的图形,外边框可以围成一个大正方形,则这个大正方形的面积为______。(用含$m$的代数式表示)
(2) 将一个正方形 A 和一个正方形 B 组合成图(3)的图形,外边框可以围成一个大正方形,用两种不同的方法表示这个大正方形的面积为______或______,从而可以得到一个乘法公式为______。
(3) 将正方形 A、B、C 各一个组合成图(4)的图形,外边框可以围成一个大正方形,类比(2)的思路进行思考,请写出得到的等式。

(1) 用两个正方形 A 组合成图(2)的图形,外边框可以围成一个大正方形,则这个大正方形的面积为______。(用含$m$的代数式表示)
(2) 将一个正方形 A 和一个正方形 B 组合成图(3)的图形,外边框可以围成一个大正方形,用两种不同的方法表示这个大正方形的面积为______或______,从而可以得到一个乘法公式为______。
(3) 将正方形 A、B、C 各一个组合成图(4)的图形,外边框可以围成一个大正方形,类比(2)的思路进行思考,请写出得到的等式。
答案:
7.[解]
(1)由题意得大正方形的边长为$2m$,则面积为$(2m)^{2}=4m^{2}$,故答案为$4m^{2}$.
(2)方法一:这个大正方形的边长为$m + n$,则这个大正方形的面积为$(m + n)^{2}$;方法二:因为这个大正方形的面积等于两个小正方形的面积与两个小长方形的面积之和,所以这个大正方形的面积为$m^{2}+n^{2}+2mn$,从而可以得到一个乘法公式为$(m + n)^{2}=m^{2}+n^{2}+2mn$.故答案为$(m + n)^{2}$,$m^{2}+n^{2}+2mn$,$(m + n)^{2}=m^{2}+n^{2}+2mn$.
(3)方法一:这个大正方形的边长为$m + n + p$,则这个大正方形的面积为$(m + n + p)^{2}$;方法二:因为这个大正方形的面积等于三个小正方形的面积与六个小长方形的面积之和,所以这个大正方形的面积为$m^{2}+n^{2}+p^{2}+2mn+2mp + 2np$,则得到的等式为$(m + n + p)^{2}=m^{2}+n^{2}+p^{2}+2mn+2mp + 2np$.
(1)由题意得大正方形的边长为$2m$,则面积为$(2m)^{2}=4m^{2}$,故答案为$4m^{2}$.
(2)方法一:这个大正方形的边长为$m + n$,则这个大正方形的面积为$(m + n)^{2}$;方法二:因为这个大正方形的面积等于两个小正方形的面积与两个小长方形的面积之和,所以这个大正方形的面积为$m^{2}+n^{2}+2mn$,从而可以得到一个乘法公式为$(m + n)^{2}=m^{2}+n^{2}+2mn$.故答案为$(m + n)^{2}$,$m^{2}+n^{2}+2mn$,$(m + n)^{2}=m^{2}+n^{2}+2mn$.
(3)方法一:这个大正方形的边长为$m + n + p$,则这个大正方形的面积为$(m + n + p)^{2}$;方法二:因为这个大正方形的面积等于三个小正方形的面积与六个小长方形的面积之和,所以这个大正方形的面积为$m^{2}+n^{2}+p^{2}+2mn+2mp + 2np$,则得到的等式为$(m + n + p)^{2}=m^{2}+n^{2}+p^{2}+2mn+2mp + 2np$.
查看更多完整答案,请扫码查看


