《2025年初中必刷题八年级数学上册华师大版》

一、选择题(每小题3分,共18分)
1[2024河北沧州期末]下列命题中,其逆命题是假命题的是( )

A.等腰三角形的两个底角相等
B.直角三角形中两个锐角互余
C.全等三角形的对应角相等
D.如果$√{a^2}= √{b^2},$那么a= b

答案： C 【解析】A 选项，逆命题为有两个角相等的三角形是等腰三角形，是真命题，故本选项不符合题意；B 选项，逆命题为有两个角互余的三角形是直角三角形，是真命题，故本选项不符合题意；C 选项，逆命题为对应角相等的三角形全等，是假命题，故本选项符合题意；D选项，逆命题为如果 a=b，那么√(a²)=√(b²)，是真命题，故本选项不符合题意. 故选 C.

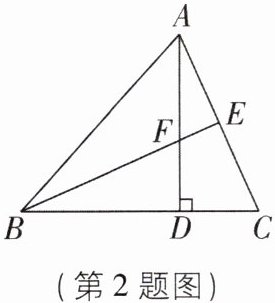
2[2025重庆期中]如图,在△ABC中,AB= BC,∠B= 48°,AD⊥BC于点D,点E为AC中点,AD与BE交于点F,则∠BFD等于( )


A.24°
B.48°
C.66°
D.76°

答案： C 【解析】
∵ 在△ABC 中，AB=BC，点 E 为AC 中点，
∴ BE 平分∠ABC，
∴ ∠DBF=1/2∠ABC=24°.
∵ AD⊥BC，
∴ ∠ADB=90°，
∴ ∠BFD=90°-∠DBF=66°. 故选 C.

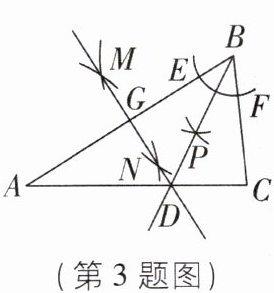
3如图,在△ABC中,∠C= 84°,点D为图中所作直线MD和射线BD与AC的交点,根据图中尺规作图痕迹,判断以下结论错误的是( )


A.AD= BD
B.∠A= ∠CBD
C.∠ABD= 32°
D.CD= GD

答案： D 【解析】由题图中尺规作图痕迹可得，BD为∠ABC 的平分线，DG 为线段 AB 的垂直平分线.
A 根据线段垂直平分线的性质可得 AD=BD，A 选项正确
B
∵ BD 为∠ABC 的平分线，
∴ ∠ABD=∠CBD.
∵ AD=BD，
∴ ∠A=∠ABD，
∴ ∠A=∠ABD=∠CBD，B 选项正确
C
∵ ∠C=84°，∠A=∠ABD=∠CBD，∠A+∠ABC+∠C=180°，
∴ 3∠ABD+84°=180°，
∴ ∠ABD=32°，C 选项正确
D 过 D 作 DH⊥BC 于 H.
∵ BP 平分∠ABC，DG⊥AB，DH⊥BC，
∴ DG=DH.
∵ DH＜CD，
∴ DG＜CD，
∴ DG≠CD，D 选项错误

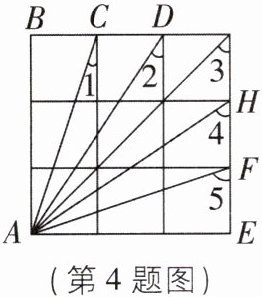
4如图,在3×3的正方形网格中,∠1+∠2+∠3+∠4+∠5等于( )

A.145°
B.180°
C.225°
D.270°

答案： C 【解析】在△ABC 和△AEF 中，{AB=AE,∠B=∠E,BC=EF,
∴ △ABC≌△AEF（SAS），
∴ ∠5=∠BCA，
∴ ∠1+∠5=∠1+∠BCA=90°. 在△ABD 和△AEH 中，{AB=AE,∠B=∠E,BD=HE,
∴ △ABD≌△AEH（SAS），
∴ ∠4=∠BDA，
∴ ∠2+∠4=∠2+∠BDA=90°.
∵ ∠3=45°，
∴ ∠1+∠2+∠3+∠4+∠5=90°+90°+45°=225°. 故选 C.

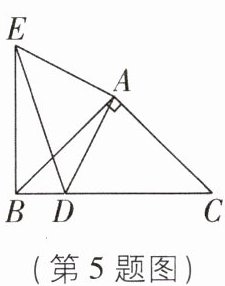
5如图,在△ABC中,∠BAC= 90°,AB= AC,BC= 2。点D在BC上,且BD:CD= 1:3。连结AD,将线段AD绕点A顺时针旋转90°得到线段AE,连结BE,DE。则△BDE的面积是( )

A.1/4
B.3/8
C.3/4
D.3/2

答案： B 【解析】
∵ ∠BAC=90°，AB=AC，
∴ ∠ABC=∠C=45°，∠BAD+∠CAD=90°.
∵ 将线段 AD 绕点 A 顺时针旋转 90°得到线段AE，
∴ AD=AE，∠DAE=∠BAD+∠BAE=90°，
∴ ∠CAD=∠BAE. 在△ADC 和△AEB 中，{AD=AE,∠CAD=∠BAE,AC=AB,
∴ △ADC≌△AEB，
∴ BE=CD，∠ABE=∠C=45°，
∴ ∠EBD=∠ABE+∠ABC=90°.
∵ BC=2，BD∶CD=1∶3，
∴ BD=2×1/4=1/2，BE=CD=2×3/4=3/2，
∴ △BDE 的面积为1/2BD·BE=1/2×1/2×3/2=3/8. 故选 B.

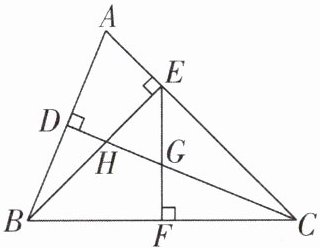
6[2025河南新乡期中]如图,在△ABC中,∠ACB= 45°,CD平分∠ACB,且CD⊥AB于点D,BE⊥AC于点E,CD与BE交于点H,EF⊥BC于点F,且与CD交于点G。则下列结论：①BF= FC；②∠ABE= ∠ACD；③BH= EH；④DB= DG,其中正确结论的序号是( )


A.①②③
B.①②④
C.②③④
D.①③④

答案： B 【解析】
∵ BE⊥AC，
∴ ∠BEC=90°.
∵ ∠ACB=45°，
∴ ∠CBE=90°-∠ACB=45°，
∴ BE=CE.
∵ EF⊥BC，
∴ BF=FC，
∴ ①正确.
∵ BE⊥AC，CD⊥AB，
∴ ∠AEB=∠ADC=90°，
∴ ∠A+∠ABE=∠A+∠ACD=90°，
∴ ∠ABE=∠ACD，
∴ ②正确. 过 H 作 HI⊥BC 于 I，如图.
∵ CD 平分∠ACB，HE⊥AC，
∴ HI=HE.
∵ BH＞HI，
∴ BH＞EH，
∴ ③不正确. 如图，连结 BG.
∵ ∠ACB=45°，CD 平分∠ACB，
∴ ∠BCD=1/2∠ACB=22.5°. 由题意可得 EF 垂直平分BC，
∴ BG=CG，
∴ ∠CBG=∠BCG=22.5°，
∴ ∠BGD=∠BCG+∠CBG=45°.
∵ CD⊥AB，
∴ ∠BDG=90°，
∴ ∠DBG=90°-∠BGD=45°，
∴ DB=DG，
∴ ④正确.
∴ 正确结论的序号是①②④. 故选 B.

二、填空题(每小题3分,共12分)
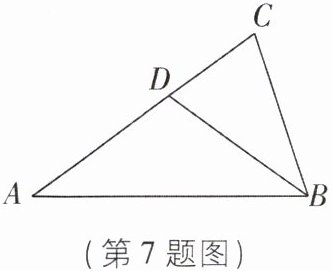
7[2025山西临汾期中]如图,在△ABC中,AB= AC,∠A= 36°,BD平分∠ABC交AC于点D。若BC= 2,则AD的长度为______。

答案： 2 【解析】
∵ AB=AC，
∴ ∠ABC=∠C.
∵ ∠A+∠ABC+∠C=180°，∠A=36°，
∴ ∠ABC=∠C=72°.
∵ BD 平分∠ABC，
∴ ∠CBD=∠ABD=36°，
∴ ∠BDC=180°-∠C-∠CBD=180°-72°-36°=72°，
∴ ∠BDC=∠C，
∴ BD=BC=2.
∵ ∠A=36°，∠ABD=36°，
∴ ∠A=∠ABD，
∴ AD=BD=2，故答案为 2.

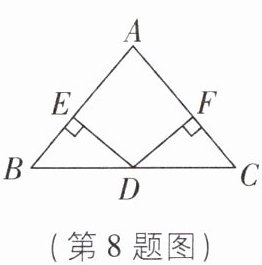
8如图,在三角形ABC中,∠B= ∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E,F,若∠BDE= 40°,则∠BAC= ______°。

答案： 80 【解析】
∵ DE⊥AB，DF⊥AC，
∴ ∠BED=∠CFD=∠AED=∠AFD=90°.
∵ D 是 BC 的中点，
∴ BD=CD. 在△BED 和△CFD 中，{∠BED=∠CFD,∠B=∠C,BD=CD,
∴ △BED≌△CFD（AAS），
∴ ∠BDE=∠CDF.
∵ ∠BDE=40°，
∴ ∠CDF=40°，
∴ ∠EDF=180°-∠BDE-∠CDF=180°-2×40°=100°，
∴ ∠BAC=360°-∠AED-∠AFD-∠EDF=360°-90°-90°-100°=80°，故答案为 80.

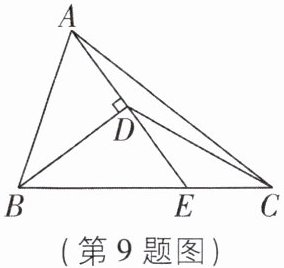
9[2025广东广州期中]如图,AE垂直于∠ABC的平分线BD,垂足为点D,且AE交BC于点E,CE= 1/3BC,若△ABC的面积为2,则△CDE的面积为______。

答案： 1/3 【解析】
∵ BD 平分∠ABC，
∴ ∠ABD=∠EBD.
∵ AE⊥BD，
∴ ∠ADB=∠EDB=90°.在△ADB 和△EDB 中，{∠ABD=∠EBD,BD=BD,∠ADB=∠EDB,
∴ △ADB≌△EDB（ASA），
∴ AD=ED.
∵ CE=1/3BC，△ABC 的面积为 2，
∴ S△AEC=1/3S△ABC=1/3×2=2/3. 又
∵ AD=ED，
∴ S△CDE=1/2S△AEC=1/2×2/3=1/3. 故答案为1/3.

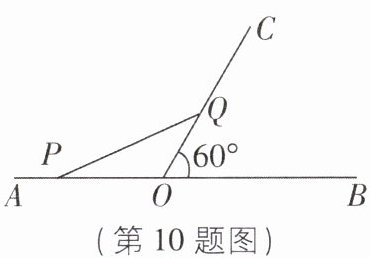
10如图,∠BOC= 60°,点A是BO延长线上的一点,OA= 10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P,Q同时出发,用t(s)表示移动的时间,当t= ______时,△POQ是等腰三角形。

答案： 10/3或10 【解析】当点 P 在射线 OA 上，PO=QO 时，△POQ 是等腰三角形，如图（1）所示. 因为 PO=AO-AP=（10-2t）cm，OQ=t cm，所以 10-2t=t，解得 t=10/3. 当 P 在射线OB 上，△POQ 是等腰三角形，∠POQ=60°，故△POQ 为等边三角形，如图（2）所示. 因为PO=AP-AO=（2t-10）cm，OQ=t cm，所以2t-10=t，解得 t=10. 综上，当 t=10/3或10 时，△POQ 是等腰三角形.