第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
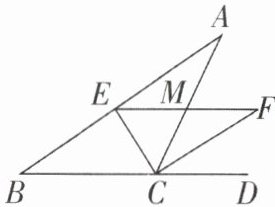
1 [2025四川攀枝花期中,中]如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF//BC交AC于M,若CM= 3,则$CE^2 + CF^2$的值为( )
A.6
B.9
C.18
D.36

A.6
B.9
C.18
D.36
答案:
D [解析]
∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE = $\frac{1}{2}$∠ACB,∠ACF = $\frac{1}{2}$∠ACD,
∴∠ECF = $\frac{1}{2}$(∠ACB + ∠ACD) = 90°,又
∵EF//BC,
∴∠ECB = ∠MEC = ∠ECM,∠DCF = ∠CFM = ∠MCF,
∴CM = EM = MF = 3,
∴EF = 6,
∴由勾股定理可知CE² + CF² = EF² = 36,故选D.
∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE = $\frac{1}{2}$∠ACB,∠ACF = $\frac{1}{2}$∠ACD,
∴∠ECF = $\frac{1}{2}$(∠ACB + ∠ACD) = 90°,又
∵EF//BC,
∴∠ECB = ∠MEC = ∠ECM,∠DCF = ∠CFM = ∠MCF,
∴CM = EM = MF = 3,
∴EF = 6,
∴由勾股定理可知CE² + CF² = EF² = 36,故选D.
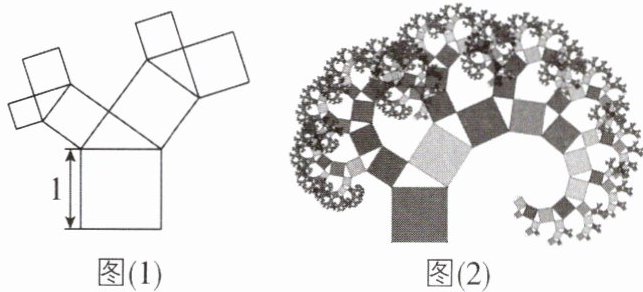
2 [2025山东枣庄期中,中]有一个边长为1的正方形,经过1次“生长”后,在它的左右“肩”上生出两个小正方形,此时这三个正方形的边围成的三角形是直角三角形,再经过1次这样的“生长”后,变成了如图(1)所示的图形。如果照此规律继续“生长”下去,它将变成如图(2)所示的“枝繁叶茂的勾股树”,请你算出“生长”了2025次后形成的图形中所有正方形的面积和是( )
A.2024
B.2025
C.2026
D.2027

A.2024
B.2025
C.2026
D.2027
答案:
C [解析]如图,由题意得,正方形A的面积为1,A,B,C三个正方形的边围成的三角形是直角三角形,
∴由勾股定理得,正方形B的面积+正方形C的面积 = 1,
∴“生长”了1次后形成的图形中所有的正方形的面积和为1 + 1 = 2.同理可得,“生长”了2次后形成的图形中所有的正方形的面积和为2 + 1 = 3,可推得“生长”了n次后形成的图形中所有的正方形的面积和为n + 1,
∴“生长”了2025次后形成的图形中所有的正方形的面积和为2026,故选C.

C [解析]如图,由题意得,正方形A的面积为1,A,B,C三个正方形的边围成的三角形是直角三角形,
∴由勾股定理得,正方形B的面积+正方形C的面积 = 1,
∴“生长”了1次后形成的图形中所有的正方形的面积和为1 + 1 = 2.同理可得,“生长”了2次后形成的图形中所有的正方形的面积和为2 + 1 = 3,可推得“生长”了n次后形成的图形中所有的正方形的面积和为n + 1,
∴“生长”了2025次后形成的图形中所有的正方形的面积和为2026,故选C.

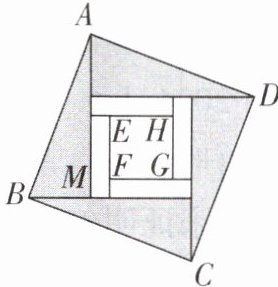
3 [新考向 传统文化][2025河南信阳期中,中]我国汉代数学家赵爽为了证明勾股定理,创制了一幅弦图,后人称其为“赵爽弦图”。弦图由四个全等的直角三角形按如图所示方式围成正方形ABCD,然后分别过较长直角边的中点作垂线,围成面积为S的小正方形EFGH。已知AM为Rt△ABM较长的直角边,若AM= 2√3EF,则正方形ABCD的面积为( )
A.14S
B.11S
C.12S
D.13S

A.14S
B.11S
C.12S
D.13S
答案:
D [解析]如图,设AM = 2a,BM = AQ = b,则AP = $\frac{1}{2}$AM = a,AB = $\sqrt{(2a)²+b²}$ = $\sqrt{4a²+b²}$,
∴正方形ABCD的面积为4a² + b².由题意易得EF = MQ - 2PQ = (AM - AQ) - 2(AP - AQ) = (2a - b) - 2(a - b) = b.
∵AM = 2$\sqrt{3}$EF,
∴2a = 2$\sqrt{3}$b,即a = $\sqrt{3}$b.
∵小正方形EFGH的面积为S,
∴b² = S,
∴正方形ABCD的面积为4a² + b² = 4($\sqrt{3}$b)² + b² = 13b² = 13S.故选D.

D [解析]如图,设AM = 2a,BM = AQ = b,则AP = $\frac{1}{2}$AM = a,AB = $\sqrt{(2a)²+b²}$ = $\sqrt{4a²+b²}$,
∴正方形ABCD的面积为4a² + b².由题意易得EF = MQ - 2PQ = (AM - AQ) - 2(AP - AQ) = (2a - b) - 2(a - b) = b.
∵AM = 2$\sqrt{3}$EF,
∴2a = 2$\sqrt{3}$b,即a = $\sqrt{3}$b.
∵小正方形EFGH的面积为S,
∴b² = S,
∴正方形ABCD的面积为4a² + b² = 4($\sqrt{3}$b)² + b² = 13b² = 13S.故选D.

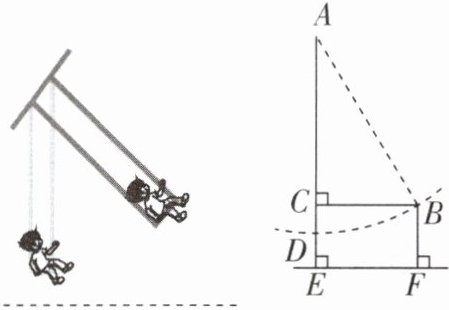
4 [2025江苏盐城期中,中]如图,有一架秋千,当它静止时,踏板离地的垂直高度DE= 0.8m,将它往前推出1.5m(即水平距离BC= 1.5m)时,秋千踏板离地的垂直高度BF= 1.3m,秋千的绳索始终拉得很直,则绳索AD长为______m。

答案:
2.5 [解析]设秋千的绳索长为x m,则AC = AD - CD = AD - (BF - DE) = x - (1.3 - 0.8) = (x - 0.5)m.在Rt△ACB中,AC² + BC² = AB²,
∴x² = (x - 0.5)² + 1.5²,解得x = 2.5,即绳索AD的长度是2.5 m.故答案为2.5.
∴x² = (x - 0.5)² + 1.5²,解得x = 2.5,即绳索AD的长度是2.5 m.故答案为2.5.
5 [2025山东青岛市北区期中,中]如图,在由若干个边长为1的小正方形组成的网格中,△ABC的顶点A,B,C均在小正方形的顶点上,BD⊥AC于点D,则BD的长为______。
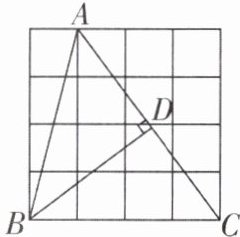

答案:
$\frac{16}{5}$ [解析]如图,AE⊥BC,
∴△ABC的面积为$\frac{1}{2}$BC×AE = $\frac{1}{2}$×4×4 = 8.由勾股定理得AC = $\sqrt{3²+4²}$ = 5,
∴$\frac{1}{2}$×5×BD = 8,解得BD = $\frac{16}{5}$,故答案为$\frac{16}{5}$

$\frac{16}{5}$ [解析]如图,AE⊥BC,
∴△ABC的面积为$\frac{1}{2}$BC×AE = $\frac{1}{2}$×4×4 = 8.由勾股定理得AC = $\sqrt{3²+4²}$ = 5,
∴$\frac{1}{2}$×5×BD = 8,解得BD = $\frac{16}{5}$,故答案为$\frac{16}{5}$

6 [较难]如图,AB= AC= 13,BP⊥CP,BP= 8,CP= 6,则阴影部分的面积为______。
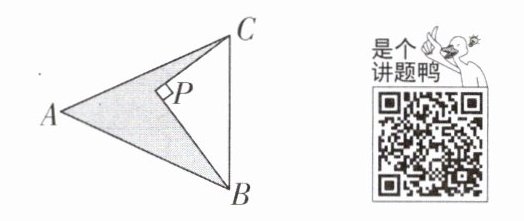

答案:
36 [解析]如图,过点A作AD⊥BC于D.在Rt△BPC中,由勾股定理得BC = $\sqrt{BP²+CP²}$ = 10.
∵AB = AC,AD⊥BC,
∴AD是△ABC的中线,
∴BD = CD = $\frac{1}{2}$BC = 5.在Rt△ABD中,由勾股定理得AD = $\sqrt{AB²−BD²}$ = $\sqrt{13²−5²}$ = 12,
∴S△ABC = $\frac{1}{2}$BC·AD = $\frac{1}{2}$×10×12 = 60.
∵S△BPC = $\frac{1}{2}$BP·PC = $\frac{1}{2}$×8×6 = 24,
∴S阴影部分 = S△ABC - S△BPC = 60 - 24 = 36.故答案为36.

36 [解析]如图,过点A作AD⊥BC于D.在Rt△BPC中,由勾股定理得BC = $\sqrt{BP²+CP²}$ = 10.
∵AB = AC,AD⊥BC,
∴AD是△ABC的中线,
∴BD = CD = $\frac{1}{2}$BC = 5.在Rt△ABD中,由勾股定理得AD = $\sqrt{AB²−BD²}$ = $\sqrt{13²−5²}$ = 12,
∴S△ABC = $\frac{1}{2}$BC·AD = $\frac{1}{2}$×10×12 = 60.
∵S△BPC = $\frac{1}{2}$BP·PC = $\frac{1}{2}$×8×6 = 24,
∴S阴影部分 = S△ABC - S△BPC = 60 - 24 = 36.故答案为36.

7 [较难]如图,已知△ABC中,∠C= 90°,AC= 8cm,BC= 6cm,P,Q是△ABC边上的两个动点,点P从点A开始沿A→C方向运动,且速度为1cm/s,点Q从点C开始沿C→B→A方向运动,且速度为2cm/s,它们同时出发,设运动的时间为t s。
(1)当t= 2时,求PQ的长。
(2)求运动几秒时,△APB是等腰三角形?
(3)当点Q在边BA上运动时,求能使△CBQ成为等腰三角形的运动时间。
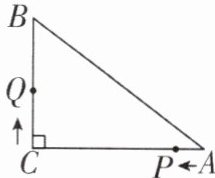

(1)当t= 2时,求PQ的长。
(2)求运动几秒时,△APB是等腰三角形?
(3)当点Q在边BA上运动时,求能使△CBQ成为等腰三角形的运动时间。


答案:
思路分析
(1)AP = t cm,CQ = 2t cm→t = 2→PQ = $\sqrt{CP²+CQ²}$
(2)△APB是等腰三角形→PA = PB→列方程求解
(3)△CBQ是等腰三角形→分类讨论→QC = QB,BQ = BC,CQ = CB→分别求解
[解]
(1)当t = 2时,AP = 2 cm,CQ = 4 cm,
∴CP = AC - AP = 8 - 2 = 6(cm).在Rt△CPQ中,PQ = $\sqrt{CP²+CQ²}$ = $\sqrt{6²+4²}$ = $\sqrt{52}$(cm),即PQ的长为$\sqrt{52}$ cm.
(2)如图
(1),当PB = PA时,△APB是等腰三角形,此时PA = PB = t cm,则PC = (8 - t)cm.在Rt△CBP中,由BC²+PC² = PB²,得6²+(8 - t)² = t²,解得t = $\frac{25}{4}$.故运动$\frac{25}{4}$s时,△APB是等腰三角形.


(3)当点Q在边BA上运动时,BQ = (2t - 6)cm.
①如图
(2),当QC = QB时,∠B = ∠BCQ.
∵∠B + ∠A = ∠BCQ + ∠ACQ = 90°,
∴∠A = ∠ACQ,
∴AQ = CQ,
∴AQ = BQ.在Rt△ABC中,BA = $\sqrt{BC²+CA²}$ = $\sqrt{6²+8²}$ = 10(cm),
∴AQ = CQ = BQ = 5 cm,
∴2t - 6 = 5,解得t = 5.5.
②如图
(3),当BQ = BC时,2t - 6 = 6,解得t = 6.


③当CQ = CB时,如图
(4),过点C作CN⊥AB,垂足为N,则$\frac{1}{2}$AC·BC = $\frac{1}{2}$AB·CN,
∴$\frac{1}{2}$×8×6 = $\frac{1}{2}$×10×CN,解得CN = $\frac{24}{5}$cm,
∴BN = $\sqrt{BC²−CN²}$ = $\sqrt{6²−(\frac{24}{5})²}$ = $\frac{18}{5}$(cm),
∴BQ = $\frac{36}{5}$cm,
∴2t - 6 = $\frac{36}{5}$,解得t = $\frac{33}{5}$.
综上所述,当运动时间为5.5s或6s或$\frac{33}{5}$s 时,△BCQ是等腰三角形。
思路分析
(1)AP = t cm,CQ = 2t cm→t = 2→PQ = $\sqrt{CP²+CQ²}$
(2)△APB是等腰三角形→PA = PB→列方程求解
(3)△CBQ是等腰三角形→分类讨论→QC = QB,BQ = BC,CQ = CB→分别求解
[解]
(1)当t = 2时,AP = 2 cm,CQ = 4 cm,
∴CP = AC - AP = 8 - 2 = 6(cm).在Rt△CPQ中,PQ = $\sqrt{CP²+CQ²}$ = $\sqrt{6²+4²}$ = $\sqrt{52}$(cm),即PQ的长为$\sqrt{52}$ cm.
(2)如图
(1),当PB = PA时,△APB是等腰三角形,此时PA = PB = t cm,则PC = (8 - t)cm.在Rt△CBP中,由BC²+PC² = PB²,得6²+(8 - t)² = t²,解得t = $\frac{25}{4}$.故运动$\frac{25}{4}$s时,△APB是等腰三角形.


(3)当点Q在边BA上运动时,BQ = (2t - 6)cm.
①如图
(2),当QC = QB时,∠B = ∠BCQ.
∵∠B + ∠A = ∠BCQ + ∠ACQ = 90°,
∴∠A = ∠ACQ,
∴AQ = CQ,
∴AQ = BQ.在Rt△ABC中,BA = $\sqrt{BC²+CA²}$ = $\sqrt{6²+8²}$ = 10(cm),
∴AQ = CQ = BQ = 5 cm,
∴2t - 6 = 5,解得t = 5.5.
②如图
(3),当BQ = BC时,2t - 6 = 6,解得t = 6.


③当CQ = CB时,如图
(4),过点C作CN⊥AB,垂足为N,则$\frac{1}{2}$AC·BC = $\frac{1}{2}$AB·CN,
∴$\frac{1}{2}$×8×6 = $\frac{1}{2}$×10×CN,解得CN = $\frac{24}{5}$cm,
∴BN = $\sqrt{BC²−CN²}$ = $\sqrt{6²−(\frac{24}{5})²}$ = $\frac{18}{5}$(cm),
∴BQ = $\frac{36}{5}$cm,
∴2t - 6 = $\frac{36}{5}$,解得t = $\frac{33}{5}$.
综上所述,当运动时间为5.5s或6s或$\frac{33}{5}$s 时,△BCQ是等腰三角形。
查看更多完整答案,请扫码查看


