《2025年初中必刷题八年级数学上册华师大版》

1 [2025 河南周口质检,中]若$a(x^{m}y^{4})^{3}÷(3x^{2}y^{n})^{2}= 2x^{5}y^{4}$,则 ( )

A.$a= 6,m= 5,n= 0$
B.$a= 18,m= 3,n= 0$
C.$a= 18,m= 3,n= 1$
D.$a= 18,m= 3,n= 4$

答案： D【解析】$a(x^{m}y^{4})^{3}÷(3x^{2}y^{n})^{2}=2x^{5}y^{4}$，即$ax^{3m}y^{12}÷9x^{4}y^{2n}=2x^{5}y^{4}$，$\therefore \frac {a}{9}x^{3m-4}y^{12-2n}=2x^{5}y^{4}$，$\therefore \frac {a}{9}=2,3m-4=5,12-2n=4$，解得$a=18,m=3,n=4$．故选D．

2 [2025 黑龙江绥化期中,中]计算$(a-b)(a+b)\cdot (a^{2}+b^{2})(a^{4}+b^{4})$的结果为 ( )

A.$a^{4}-b^{4}$
B.$a^{6}+b^{6}$
C.$a^{6}-b^{6}$
D.$a^{8}-b^{8}$

答案： D【解析】$(a-b)(a+b)(a^{2}+b^{2})(a^{4}+b^{4})=(a^{2}-b^{2})(a^{2}+b^{2})(a^{4}+b^{4})=(a^{4}-b^{4})(a^{4}+b^{4})=a^{8}-b^{8}$，故选D．

3 [2024 山东临沂期末,中]计算$\sqrt {162^{2}-64^{2}-98^{2}}$的值为 ( )

A.0
B.2
C.56
D.112

答案： D【解析】$\sqrt {162^{2}-64^{2}-98^{2}}=\sqrt {(162+64)×(162-64)-98^{2}}=\sqrt {226×98-98^{2}}=\sqrt {98×(226-98)}=\sqrt {98×128}=\sqrt {49×2×64×2}=7×2×8=112$．故选D．

4 [2024 山西大同模拟,中]数形结合是数学解题中常用的思想方法,数形结合的思想可以使某些抽象的数学问题直观化、生动化,有助于把握数学问题的本质.在学习整式运算乘法公式的过程中,对于每个公式的推导,教材编写者都运用了图形面积来加以验证.下列图形中,不能借助图形面积验证$(a+b)(a-b)= a^{2}-b^{2}$的正确性的是 ( )

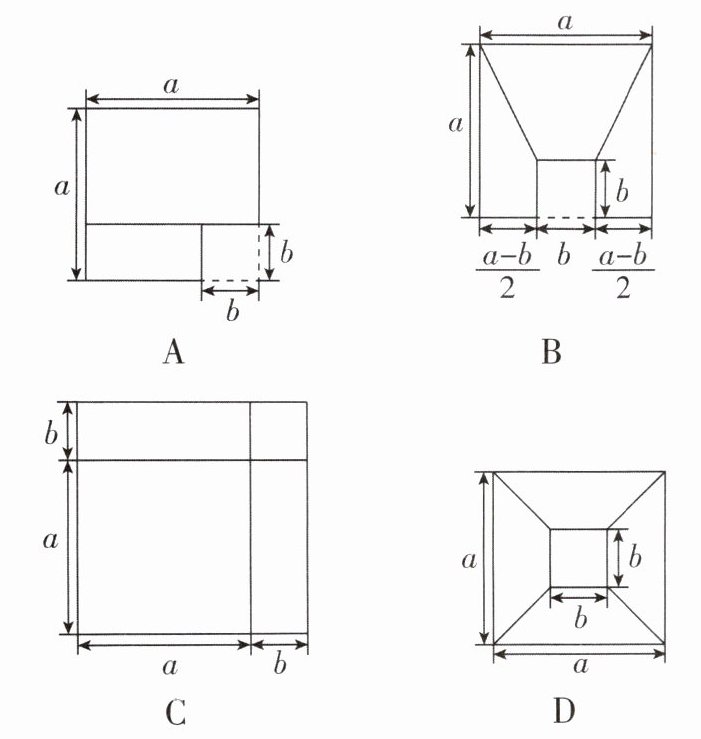
答案： C【解析】A选项，大正方形的面积为$a^{2}$，小正方形的面积为$b^{2}$，两个长方形的面积之和为$(a-b)b+a(a-b)=(a+b)(a-b)=a^{2}-b^{2}$，故此选项可以验证$(a+b)(a-b)=a^{2}-b^{2}$，不符合题意；B选项，大正方形的面积为$a^{2}$，小正方形的面积为$b^{2}$，三个梯形的面积之和为$2×\frac {a+b}{2}·\frac {a-b}{2}+a(a-b)=(a+b)(a-b)=a^{2}-b^{2}$，故此选项可以验证$(a+b)(a-b)=a^{2}-b^{2}$，不符合题意；C选项，两个较小的正方形面积分别为$a^{2},b^{2}$，两个长方形的面积之和为$2ab$，大正方形的面积为$(a+b)^{2}=a^{2}+b^{2}+2ab$，不能验证$(a+b)(a-b)=a^{2}-b^{2}$，符合题意；D选项，大正方形的面积为$a^{2}$，小正方形的面积为$b^{2}$，四个梯形的面积之和为$4×\frac {a+b}{2}·\frac {a-b}{2}=(a+b)(a-b)=a^{2}-b^{2}$，故此选项可以验证$(a+b)(a-b)=a^{2}-b^{2}$，不符合题意．故选C．

5 [2025 重庆万州区期中,中]已知 a,b,c 分别是$△ABC$的三边长,若$a^{2}+2ab+b^{2}= c^{2}+80,a+b-c= 4$,则 c 的值是 ( )

A.20
B.16
C.8
D.4

答案： C【解析】$\because a^{2}+2ab+b^{2}=c^{2}+80$，$\therefore (a+b)^{2}-c^{2}=80$，$\therefore (a+b+c)(a+b-c)=80$．$\because a+b-c=4$，① $\therefore 4(a+b+c)=80$，$\therefore a+b+c=20$，② ②-①得$c=8$．故选C．

6 [2024 重庆九龙坡区期末,中]如果多项式$A= x^{2}+2xy+2y^{2}-4y+2019$,则 A 的最小值是____.

答案： 2015【解析】$A=x^{2}+2xy+2y^{2}-4y+2019=x^{2}+2xy+y^{2}+y^{2}-4y+4+2015=(x+y)^{2}+(y-2)^{2}+2015$．$\because (x+y)^{2}\geq 0$，$(y-2)^{2}\geq 0$，$\therefore A$的最小值是2015．故答案为2015．

7 [较难]同号两实数 a,b 满足$a^{2}+b^{2}= 4-2ab$,若$a-b$为整数,则 ab 的值为____.

答案： 1或$\frac {3}{4}$【解析】$\because a^{2}+b^{2}=4-2ab$，$\therefore (a+b)^{2}=4$，$\therefore (a-b)^{2}=(a+b)^{2}-4ab=4-4ab\geq 0$，$\therefore ab\leq 1$．又$\because ab＞0$，$\therefore 0＜ab\leq 1$，$\therefore 0\leq 4-4ab＜4$．$\because a-b$为整数，$\therefore 4-4ab$为平方数，$\therefore 4-4ab=1$或0，解得$ab=\frac {3}{4}$或1．故答案为1或$\frac {3}{4}$．

8 [较难]已知$a= 2023x+2022,b= 2023x+2023,c= 2023x+2024$,那么$a^{2}+b^{2}+c^{2}-ab-bc-ac$的值为____.

答案： 3【解析】$\because a=2023x+2022$，$b=2023x+2023$，$c=2023x+2024$，$\therefore a-b=-1$，$b-c=-1$，$a-c=-2$，$\therefore a^{2}+b^{2}+c^{2}-ab-bc-ac=\frac {1}{2}(2a^{2}+2b^{2}+2c^{2}-2ab-2bc-2ac)=\frac {1}{2}[(a-b)^{2}+(b-c)^{2}+(a-c)^{2}]=\frac {1}{2}[(-1)^{2}+(-1)^{2}+(-2)^{2}]=3$，故答案为3．

9 新考法[2025 广东深圳期中,中]某科技馆的“数理世界”展厅中一款互动游戏的解锁密码被设计成如图所示的数学问题.小东在参观时认真思索,输入密码后顺利解锁游戏,则他输入的密码是____.
账号:shu li shi jie
$[x^{19}y^{8}z^{8}]= 1988,[x^{2}yz\cdot x^{3}y]= 521,[x^{10}y^{2}z^{3}÷x]= 923,[(x^{5})^{5}y^{4}z^{3}÷x^{5}y^{2}z]= $密码

答案： 2022【解析】由题意可知密码为$x,y,z$的指数合在一起．$\because [(x^{5})^{5}y^{4}z^{3}÷x^{5}y^{2}z]=[x^{20}y^{2}z^{2}]$，$\therefore$密码是2022，故答案为2022．

10 [2025 广西柳州质检,中]已知多项式$x^{2}+bx+c$(其中 b,c 是常数)既是多项式$x^{4}+6x^{2}+25$的因式,也是多项式$3x^{4}+4x^{2}+28x+5$的因式,则当$x= 1$时,$x^{2}+bx+c$的值为____.

答案： 4【解析】$\because$多项式$x^{2}+bx+c$（其中$b,c$是常数）既是多项式$x^{4}+6x^{2}+25$的因式，也是多项式$3x^{4}+4x^{2}+28x+5$的因式，$\therefore$也必定是$3(x^{4}+6x^{2}+25)$与$3x^{4}+4x^{2}+28x+5$差的一个因式．$\because 3(x^{4}+6x^{2}+25)-(3x^{4}+4x^{2}+28x+5)=14(x^{2}-2x+5)$，$\therefore x^{2}-2x+5=x^{2}+bx+c$，$\therefore b=-2$，$c=5$，$\therefore$当$x=1$时，$x^{2}+bx+c=1^{2}-2+5=4$，故答案为4．