《2025年初中必刷题八年级数学上册华师大版》

1[2025湖南怀化期中]已知△ABC的六个元素，下面甲、乙、丙三个三角形中标出了某些元素，则与△ABC全等的三角形是（ ）


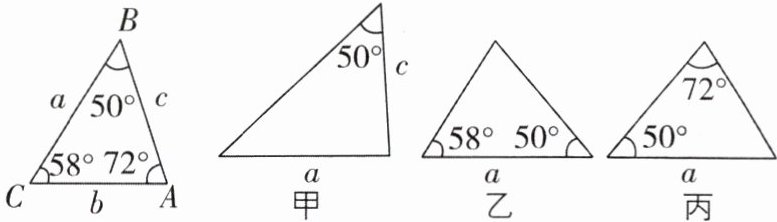
A.只有乙
B.只有丙
C.甲和乙
D.乙和丙

答案： 1.D　[解析]根据题图可知，可利用ASA证明乙三角形与△ABC全等；可利用AAS证明丙三角形与△ABC全等；无法证明甲三角形与△ABC全等，
∴甲、乙、丙三个三角形中和△ABC全等的是乙和丙，故选D.

2[2025河南洛阳期中]如图，AC与BD相交于点O，OD=OC，有以下4个条件：①∠C=∠D；②AD=BC；③∠DAO=∠CBO；④OA=OB.从这4个条件中任选一个，能使△DAO≌△CBO的条件个数为（ ）

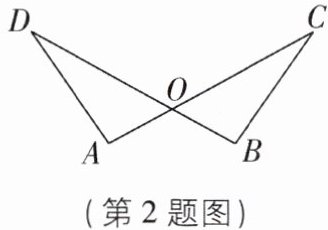
A.2
B.3
C.4
D.1

答案： 2.B　[解析]①在△DAO与△CBO中，∠D=∠C，OD=OC，∠DOA=∠COB，
∴△DAO≌△CBO(ASA)，符合题意；②添加AD=BC不能判定△DAO≌△CBO，不符合题意；③在△DAO与△CBO中，∠DAO=∠CBO，∠DOA=∠COB，OD=OC，
∴△DAO≌△CBO(AAS)，符合题意；④在△DAO与△CBO中，OA=OB，∠DOA=∠COB，OD=OC，
∴△DAO≌△CBO(SAS)，符合题意.
∴①③④符合题意，故选B.

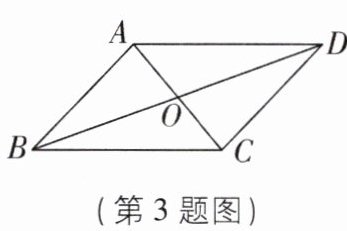
3如图，在四边形ABCD中，对角线AC，BD相交于点O，OA=OC，当添加条件______时，可依据“SAS”证明△AOB≌△COD；当添加条件______时，可依据“AAS”证明△AOB≌△COD.

答案： 3.OB=OD AB//CD(答案不唯一)　[解析]添加条件OB=OD时，在△AOB和△COD中，AO=CO，∠AOB=∠COD，BO=DO，
∴△AOB≌△COD(SAS).添加条件AB//CD时，
∵AB//CD，
∴∠ABO=∠CDO，∠BAO=∠DCO.在△AOB和△COD中，∠ABO=∠CDO，∠BAO=∠DCO，OA=OC，
∴△AOB≌△COD(AAS).故答案为OB=OD，AB//CD(答案不唯一).

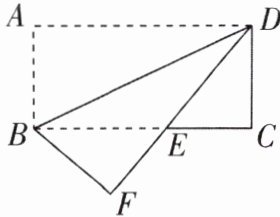
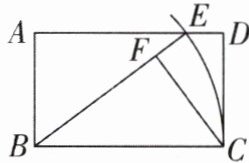
4[2025陕西汉中期末]如图，将长方形纸片ABCD沿对角线BD折叠，使点A落在平面上的F点处，DF交BC于点E. 求证：△DCE≌△BFE.

答案： 4.[证明]
∵四边形ABCD为长方形，
∴AB=CD，∠BAD=∠C=90°.
∵将长方形纸片ABCD沿对角线BD折叠，使点A落在平面上的F点处，
∴BF=AB=CD，∠BFE=∠BAD=∠C=90°.又
∵∠DEC=∠BEF，
∴△DCE≌△BFE (AAS).

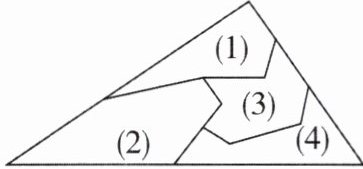
5[2025山东德州期中]一名工作人员不慎将一块三角形模具打碎成了如图所示的四块，他需要去商店再配一块与原来大小和形状完全相同的模具. 现只能拿两块去配，其中可以配出符合要求的模具的是（ ）

A.(1)(3)
B.(3)(4)
C.(1)(4)
D.(1)(2)

答案： 5.D　[解析]由题图可知
(1)
(2)或
(2)
(4)可以组成两个完整的角和两个角的夹边，根据ASA可以配出大小、形状完全相同的三角形，符合题意；其他组合均不能配出大小、形状完全相同的三角形，故选D.

6如图，在四边形ABCD中，∠ABC=90°，AD//BC，以B为圆心，BC长为半径画弧，与AD相交于点E，连结BE，过点C作CF⊥BE，垂足为F. 若AE=8，BC=10，则EF的长为______.

答案： 6.2　[解析]由题可知BE=BC=10.
∵∠ABC=90°，AD//BC，
∴∠A=180°−∠ABC=90°，∠AEB=∠FBC.
∵CF⊥BE，
∴∠BFC=90°，
∴∠A=∠BFC.在△AEB和△FBC中，∠A=∠BFC，∠AEB=∠FBC，BE=CB，
∴△AEB≌△FBC(AAS)，
∴BF=AE=8，
∴EF=BE−BF=10−8=2.故答案为2.

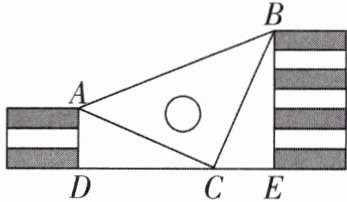
7如图，王强同学用10块高度都是2cm的相同的长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板(AC=BC，∠ACB=90°)，点C在DE上，点A和B分别与木墙的顶端重合.
(1)求证：△ADC≌△CEB；
(2)求两堵木墙之间的距离.

答案： 7.
(1)[证明]由题意得AC=BC，∠ACB=90°，AD⊥DE，BE⊥DE，
∴∠ADC=∠CEB=90°，
∴∠ACD+∠BCE=∠ACD+∠DAC=90°，
∴∠BCE=∠DAC.在△ADC和△CEB中，∠ADC=∠CEB，∠DAC=∠BCE，AC=BC，
∴△ADC≌△CEB(AAS).
(2)[解]由题意得AD=2×3=6(cm)，BE=7×2=14(cm).
∵△ADC≌△CEB，
∴EC=AD=6cm，DC=BE=14cm，
∴DE=DC+CE=20cm.答:两堵木墙之间的距离为20cm.