《2025年初中必刷题八年级数学上册华师大版》

1 [2024 云南昆明盘龙区校级期末] 计算 $ mn \cdot \left( \frac { 1 } { 2 } m - 3 m n ^ { 2 } \right) $,结果正确的是( )

A.$ \frac { 1 } { 2 } m n - 3 m ^ { 2 } n ^ { 2 } $
B.$ \frac { 1 } { 2 } m ^ { 2 } n - 3 m ^ { 2 } n ^ { 3 } $
C.$ \frac { 1 } { 2 } m n ^ { 2 } - 3 m n ^ { 3 } $
D.$ m ^ { 2 } n - 3 m n ^ { 2 } $

答案： B　[解析]mn.($\frac{1}{2}$m−3mn²)=mn.$\frac{1}{2}$m−mn.3mn²=$\frac{1}{2}$m²n−3m²n³.故选B.

2 下列运算中,正确的是( )

A.$ - 2 x ( 3 x ^ { 2 } y - 2 x y ) = - 6 x ^ { 3 } y - 4 x ^ { 2 } y $
B.$ 2 x y ^ { 2 } ( - x ^ { 2 } + 2 y ^ { 2 } + 1 ) = - 4 x ^ { 3 } y ^ { 4 } $
C.$ ( 3 a b ^ { 2 } - 2 a b ) \cdot a b c = 3 a ^ { 2 } b ^ { 3 } - 2 a ^ { 2 } b ^ { 2 } $
D.$ ( a b ) ^ { 2 } ( 2 a b ^ { 2 } - c ) = 2 a ^ { 3 } b ^ { 4 } - a ^ { 2 } b ^ { 2 } c $

答案： D　[解析]A选项,−2x(3x²y−2xy)=−6x³y+4x²y,故本选项错误;B选项,2xy²(−x²+2y²+1)=−2x³y²+4xy⁴+2xy²,故本选项错误;C选项,(3ab²−2ab).abc=3a²b³c−2a²b²c,故本选项错误;D选项,(ab)²(2ab²−c)=a²b².(2ab²−c)=2a³b⁴−a²b²c,故本选项正确.故选D.

3 [2025 四川南充高坪区期末] 已知 $ m - 2 n = 1 $,则 $ 2 n ( m + 1 ) - m ( 1 + 2 n ) + 3 $ 的值为( )

A.4
B.2
C.-4
D.-2

答案： B　[解析]
∵m−2n=1,
∴2n−m=−1,
∴原式=2mn+2n−m−2mn+3=2n−m+3=−1+3=2.故选B.

4 [2024 山西临汾期末] 某同学计算一个多项式乘 $ - 3 x ^ { 2 } $ 时,因抄错符号,算成了加上 $ - 3 x ^ { 2 } $,得到的答案是 $ x ^ { 2 } - \frac { 1 } { 2 } x + 1 $,那么正确的计算结果是______.

答案： −12x⁴+$\frac{3}{2}$x³−3x²　[解析]这个多项式是$\left( x^2 - \frac{1}{2}x + 1 \right) - (-3x^2) = 4x^2 - \frac{1}{2}x + 1$，正确的计算结果是$\left( 4x^2 - \frac{1}{2}x + 1 \right)(-3x^2) = -12x^4 + \frac{3}{2}x^3 - 3x^2$.故答案为−12x⁴+$\frac{3}{2}$x³−3x².

5 定义三角 $ \begin{array} { c } { a } \\ { b \quad c } \end{array} $ 表示 $ 3 a b c $,方框 $ \begin{array} { c } { x \quad w } \\ { y \quad z } \end{array} $ 表示 $ x z + w y $,则 $ \begin{array} { c } { m } \\ { n \quad 3 } \end{array} × \begin{array} { c } { 4 \quad n } \\ { 5 \quad 2 m } \end{array} $ 的结果为______.

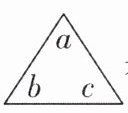
答案：
72m²n + 45mn²　[解析]根据题意,得 =9mn×(8m + 5n) = 72m²n + 45mn².故答案为72m²n + 45mn².

6 [2025 上海宝山区期中] 计算：
(1)$ \left( - \frac { 1 } { 2 } x y ^ { 2 } \right) ( 3 x ^ { 2 } y - 4 x y + 1 ) $.
(2)$ 2 x ( x - y ) - 2 y ( y - x ) $.
(3)$ ( a ^ { 2 } - 2 a b + 3 ) \cdot ( - 3 a ^ { 2 } ) ^ { 2 } $.

答案：
(1)原式$= \left( -\frac{1}{2}xy^2 \right)\cdot 3x^2y - \left( -\frac{1}{2}xy^2 \right)\cdot 4xy + \left( -\frac{1}{2}xy^2 \right)\cdot 1 = -\frac{3}{2}x^3y^3 + 2x^2y^3 - \frac{1}{2}xy^2$.
(2)原式$= 2x^2 - 2xy - 2y^2 + 2xy = 2x^2 - 2y^2$.
(3)原式$= (a^2 - 2ab + 3)\cdot 9a^4 = 9a^6 - 18a^5b + 27a^4$.
易错警示：注意单项式与单项式相乘时，积的正负由两个单项式的系数的正负确定：同号得正，异号得负.

7 [2025 山西临汾质检] 如图为 “L” 形钢材的截面图,要计算其截面面积,下列给出的算式中,错误的是( )

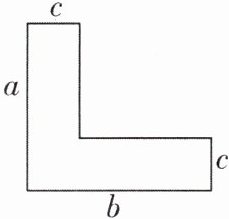
A.$ a b - c ^ { 2 } $
B.$ a c + ( b - c ) c $
C.$ b c + ( a - c ) c $
D.$ a c + b c - c ^ { 2 } $

答案： A　[解析]由题图可得，“L”形钢材的截面面积为$ac + (b - c)c = ac + bc - c^2$，故选项B、D正确，不符合题意；“L”形钢材的截面面积还可表示为$bc + (a - c)c = bc + ac - c^2$，故选项C正确，不符合题意.故选A.

8 已知 $ ( - 2 x ^ { 2 } ) ( 3 x ^ { 2 } - a x - 6 ) - 3 x ^ { 3 } + x ^ { 2 } $ 中不含 $ x $ 的三次项,则 $ a $ 的值为______.

答案： $\frac{3}{2}$　[解析](−2x²)(3x²−ax−6)−3x³+x²=−6x⁴+2ax³+12x²−3x³+x²=−6x⁴+(2a−3)x³+13x².因为该式中不含x的三次项,所以2a−3=0,解得a=$\frac{3}{2}$.

9 [2025 重庆万州区期中] 学习代数式求值时,遇到这样一类题：“已知代数式 $ a x - y + 6 + 3 x - 5 y - 1 $ 的值与 $ x $ 的取值无关,求 $ a $ 的值”. 通常的解题方法是把 $ a $ 看成常数合并同类项,因为代数式的值与 $ x $ 的取值无关,所以含 $ x $ 项的系数为 0,即原式 $ = ( a + 3 ) x - 6 y + 5 $,所以 $ a + 3 = 0 $,则 $ a = - 3 $. 根据上述方法解答下列问题：
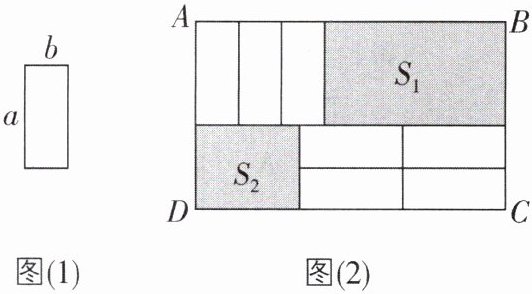
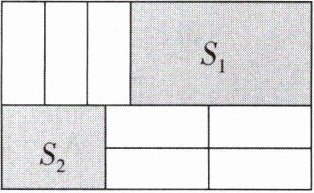
(1)已知 $ A = 2 x ^ { 2 } - ( 1 - 3 n ) x $,$ B = - x ^ { 2 } + n x - 1 $,且 $ 3 A + 6 B $ 的值与 $ x $ 的取值无关,求 $ n $ 的值.
(2)有 7 张如图(1)所示的小长方形纸片,长为 $ a $,宽为 $ b $,按照如图(2)所示的方式不重叠地放在大长方形 $ A B C D $ 内,大长方形中未被覆盖的两个部分(图中阴影部分)的面积分别为 $ S _ { 1 } $,$ S _ { 2 } $. 设 $ A B = x $,当 $ A B $ 的长变化时,$ 3 S _ { 1 } - 4 S _ { 2 } $ 的值始终保持不变,请求出 $ \frac { a } { b } $ 的值.

答案：
(1)
∵A=2x²−(1−3n)x,B=−x²+nx−1,
∴3A+6B=3[2x²−(1−3n)x]+6(−x²+nx−1)=3(2x²−x+3nx)+6(−x²+nx−1)=6x²−3x+9nx−6x²+6nx−6=(−3+9n+6n)x−6=(15n−3)x−6.
∵3A+6B的值与x的取值无关，
∴15n−3=0,
∴n=$\frac{1}{5}$.
(2)已知AB = x，由题图可知$S_1 = a(x - 3b)$，$S_2 = 2b(x - 2a)$，
∴$3S_1 - 4S_2 = 3a(x - 3b) - 4×2b\cdot (x - 2a) = (3a - 8b)x + 7ab$.
∵当AB的长变化时，$3S_1 - 4S_2$的值始终保持不变，
∴$3S_1 - 4S_2$的值与x的取值无关，
∴3a - 8b = 0，
∴3a = 8b，
∴$\frac{a}{b} = \frac{8}{3}$.