《2025年初中必刷题八年级数学上册华师大版》

1 [2025 河南洛阳新安期末] 用反证法证明“若 $ab = 0$,则 $a$,$b$ 中至少有一个为 $0$”时,第一步应假设( )

A.$a = 0$,$b = 0$
B.$a \neq 0$,$b \neq 0$
C.$a \neq 0$,$b = 0$
D.$a = 0$,$b \neq 0$

答案： B 【解析】用反证法证明"若ab=0,则a,b中至少有一个为0"时,第一步应假设a≠0,b≠0. 故选 B.

2 [2024 浙江衢州期末] 用反证法证明“在直角三角形中至少有一个锐角小于或等于 $45^{\circ}$”,应假设两个锐角( )

A.都大于 $45^{\circ}$
B.都小于 $45^{\circ}$
C.都不大于 $45^{\circ}$
D.都不小于 $45^{\circ}$

答案： A 【解析】用反证法证明"在直角三角形中至少有一个锐角小于或等于45°",应假设两个锐角都大于45°,故选 A.

3 用反证法证明“在 $\triangle ABC$ 中,$AB = c$,$BC = a$,$CA = b$,$\angle C ＞ \angle B ＞ \angle A$ 且 $\angle C \neq 90^{\circ}$,那么 $a^{2}+b^{2} \neq c^{2}$”时,应先假设( )

A.$a^{2}+b^{2}= c^{2}$
B.$a^{2}+b^{2}＞c^{2}$
C.$a^{2}+b^{2}＜c^{2}$
D.$a^{2}+b^{2}＞c^{2}$ 或 $a^{2}+b^{2}＜c^{2}$

答案： A 【解析】用反证法证明"在△ABC中,AB=c,BC=a,CA=b,∠C＞∠B＞∠A且∠C≠90°,那么$a^{2}+b^{2}\neq c^{2}$"时,应先假设$a^{2}+b^{2}=c^{2}$,故选 A.

4 如图,在 $\triangle ABC$ 中,$AB = AC$,点 $P$ 为 $\triangle ABC$ 内一点,连结 $PA$,$PB$,$PC$,$\angle APB \neq \angle APC$,求证：$PB \neq PC$。用反证法证明时,第一步应假设( )


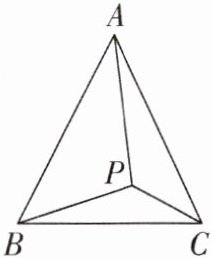
A.$AB \neq AC$
B.$PB = PC$
C.$\angle APB = \angle APC$
D.$\angle PBC \neq \angle PCB$

答案： B 【解析】用反证法证明时,应先假设结论不成立,即第一步先假设PB=PC. 故选 B.

5 [2024 山西临汾期末] 反证法是数学证明的一种重要方法。请将下面运用反证法进行证明的过程补全。
已知：在 $\triangle ABC$ 中,$AB = AC$。求证：$\angle B ＜ 90^{\circ}$。
证明：假设______。
$\because AB = AC$,
$\therefore \angle B = \angle C \geqslant 90^{\circ}$,
$\therefore \angle A + \angle B + \angle C ＞ 180^{\circ}$,
这与______,
$\therefore$ ______不成立,
$\therefore \angle B ＜ 90^{\circ}$。

答案： ∠B≥90° 三角形的内角和定理(或三角形的内角和等于180°)相矛盾 此假设

6 [2025 山西临汾期末] 如图,在 $\triangle ABC$ 中,$AC ＞ AB$,$AD$ 是 $\triangle ABC$ 的中线,$AE \perp BC$ 于点 $E$,用反证法证明：点 $D$ 与点 $E$ 不重合。

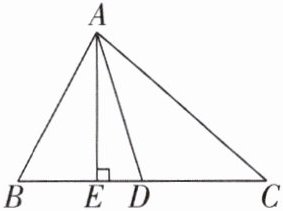
答案： 【证明】假设点 D 与点 E 重合.
∵ AD 是△ABC的中线,AE⊥BC,
∴ AD 垂直平分 BC,
∴ AB=AC,与AC＞AB相矛盾,
∴ 假设不成立,
∴ 点 D与点 E 不重合.

7 阅读下列内容,回答问题。
题目：在 $\text{Rt} \triangle ABC$ 中,$\angle C = 90^{\circ}$,若 $\angle A \neq 45^{\circ}$,则 $AC \neq BC$。
证明：假设 $AC = BC$,因为 $\angle A \neq 45^{\circ}$,$\angle C = 90^{\circ}$,所以 $\angle A \neq \angle B$。
所以 $AC \neq BC$,这与假设矛盾,所以 $AC \neq BC$。
上面的证明过程有没有错误？若没有错误,指出证明的方法；若有错误,请改正。

答案： 【解】有错误. 改正:假设AC=BC,则∠A=∠B. 又因为∠C=90°,所以∠B=∠A=45°,这与∠A≠45°矛盾,所以AC=BC不成立,所以AC≠BC.

8 用反证法证明：
(1)已知：$a ＜ |a|$,求证：$a$ 必为负数；
(2)求证：形如 $4n + 3$ 的整数($n$ 为整数)不能化为两个整数的平方和。

答案： 【证明】
(1)假设a不是负数,即a≥0,则|a|=a,这与已知|a|＞a相矛盾,因此假设不成立,所以a必为负数.
(２)假设形如4n+3的整数(n为整数)能化为两个整数の平方和,不妨设这两个整数为α,β,则4n+3=$α^{2}+β^{2}$.因为4n+3=(n+2)$^{2}$+(-$n^{2}$-1)≠$α^{2}+β^{2}$,所以假设不成立,故形如4n+3的整数(n为整数)不能化为两个整数的平方お.