《2025年初中必刷题八年级数学上册华师大版》

1 [中]下列各数中,一定没有平方根的是( )

A.$-a$
B.$-a^{2}+1$
C.$-a^{2}$
D.$-a^{2}-1$

答案： 1.D [解析]平方根的被开方数不能是负数。

2 [2025 河南郑州期末,中]电流通过导体时会产生热量,满足$Q = I^{2}Rt$,其中$Q$为产生的热量(单位：J),$I$为电流(单位：A),$R$为导体的电阻(单位：$\Omega$),$t$为通电时间(单位：s)。若导体的电阻为$5\Omega$,$1s$的时间导体产生 30J 的热量,则通过导体的电流$I$为( )

A.2.4A
B.$\sqrt{6}A$
C.4.8A
D.$5\sqrt{6}A$

答案： 2.B [解析]由题意可得R = 5Ω，t = 1s，Q = 30J，
∴30 = $I^2$×5×1，
∴$I^2 = 6$，
∴I = ±$\sqrt{6}$（负值不符合实际情况，舍去），
∴通过导体的电流I是$\sqrt{6}$A，故选B．

3 [2025 安徽宿州期末,中]$x^{2}+2024的平方根分别是a$,$b$,则$a + b-\frac{b}{a}$的值为( )

A.0
B.1
C.$-1$
D.2

答案： 3.B [解析]
∵$x^2 + 2024\geq2024＞0$，$x^2 + 2024$的平方根分别是a，b，
∴a，b互为相反数且都不为0，
∴a + b = 0，$\frac{b}{a}=-1$，
∴a + b - $\frac{b}{a}=0 - (-1)=1$，故选B。

4 [2025 广东肇庆期末,中]如果$\sqrt{1 - 3x}和\sqrt{y - 27}$互为相反数,那么$\sqrt{xy}$的平方根是______。

答案： 4.±$\sqrt{3}$ [解析]
∵$\sqrt{1 - 3x}\geq0$，$\sqrt{y - 27}\geq0$，且$\sqrt{1 - 3x}$和$\sqrt{y - 27}$互为相反数，
∴1 - 3x = 0，y - 27 = 0，解得$x = \frac{1}{3}$，y = 27，
∴$\sqrt{xy}=\sqrt{\frac{1}{3}×27}=\sqrt{9}=3$，
∴$\sqrt{xy}$的平方根是±$\sqrt{3}$，故答案为±$\sqrt{3}$。

5 [较难]设$S_{1}= 1+\frac{1}{1^{2}}+\frac{1}{2^{2}}$,$S_{2}= 1+\frac{1}{2^{2}}+\frac{1}{3^{2}}$,$S_{3}= 1+\frac{1}{3^{2}}+\frac{1}{4^{2}}$,…$$,$S_{n}= 1+\frac{1}{n^{2}}+\frac{1}{(n + 1)^{2}}$,则$\sqrt{S_{1}}+\sqrt{S_{2}}+…+\sqrt{S_{24}}$的值为______。

答案： 5.$\frac{624}{25}$ [解析]$\sqrt{S_1}=\sqrt{1 + 1+\frac{1}{4}}=\frac{3}{2}$，$\sqrt{S_2}=\sqrt{1+\frac{1}{4}+\frac{1}{9}}=\frac{7}{6}$，$\sqrt{S_3}=\sqrt{1+\frac{1}{9}+\frac{1}{16}}=\frac{13}{12}$，$\sqrt{S_4}=\sqrt{1+\frac{1}{16}+\frac{1}{25}}=\frac{21}{20}$，…，由规律可得$\sqrt{S_n}=1+\frac{1}{n}-\frac{1}{n + 1}$，
∴$\sqrt{S_1}+\sqrt{S_2}+…+\sqrt{S_{24}}=1 + 1-\frac{1}{2}+1+\frac{1}{2}-\frac{1}{3}+…+1+\frac{1}{24}-\frac{1}{25}=24 + 1-\frac{1}{25}=\frac{624}{25}$，故答案为$\frac{624}{25}$。

6 [较难]将尺寸如图所示的 4 块完全相同的长方形薄木板(厚度忽略不计)进行拼摆,恰好可以不重叠地摆放在如图的甲、乙两个方框内。已知薄木板的宽为 2,图甲中阴影部分的面积为 19,则图乙中$AD$的长为______。

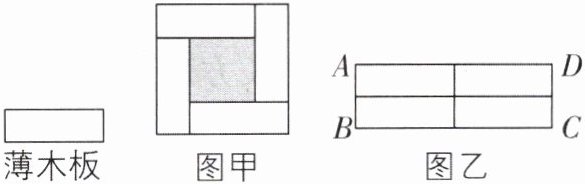
答案： 6.2($\sqrt{19}+2$) [解析]由图甲知，阴影部分的4条边长都等于薄木板的长减去2，
∴阴影部分是正方形。
∵阴影部分的面积为19，
∴阴影部分的边长为$\sqrt{19}$，
∴薄木板的长为$\sqrt{19}+2$，
∴AD = 2($\sqrt{19}+2$)，故答案为2($\sqrt{19}+2$)。

7 [2025 山东青岛质检,中]已知$x = 1 - 2a$,$y = 3a - 4$。
(1)若$x$的算术平方根为 3,求$a$的值；
(2)如果$x$,$y$是同一个数的平方根,求这个数。

答案： 7.【解】
(1)
∵x的算术平方根为3，
∴x = 9，即1 - 2a = 9，解得a = - 4。
(2)
∵x，y是同一个数的平方根，
∴x = y或x = - y，
∴1 - 2a = 3a - 4或1 - 2a = -(3a - 4)，解得a = 1或a = 3。
当a = 1时，$(1 - 2a)^2=(1 - 2)^2 = 1$；当a = 3时，$(1 - 2a)^2=(1 - 6)^2 = 25$，
∴这个数是1或25。

8 [2025 山西太原质检,中]观察表格并回答下列问题。
| $a(a ＞ 0)$ | …$$ | 0.0001 | 0.01 | 1 | 100 | 10000 | …$$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $\sqrt{a}$ | …$$ | 0.01 | $x$ | 1 | $y$ | 100 | …$$ |
(1)表格中$x= $______,$y= $______。
(2)①已知$\sqrt{6}\approx 2.45$,则$\sqrt{0.06}\approx$______；
②已知$\sqrt{0.0012}\approx 0.03464$,$\sqrt{2m}\approx 34.64$,求$m$的值。

答案： 8.【解】
(1)$x=\sqrt{0.01}=0.1$，$y=\sqrt{100}=10$，故答案为0.1，10。
(2)①由表格中数据可得，被开方数的小数点每向右移动两位，则它的算术平方根的小数点就向右移动一位。
∵$\sqrt{6}\approx2.45$，
∴$\sqrt{0.06}\approx0.245$，故答案为0.245。
②
∵$\sqrt{0.0012}\approx0.03464$，$\sqrt{2m}\approx34.64$，且0.03464的小数点向右移动三位得到34.64，
∴0.0012的小数点向右移动六位得到2m，
∴$0.0012×10^6 = 2m$，
∴m = 600。

9 [中]定义：对于三个互不相等的正整数,若其中任意两个数乘积的算术平方根都是整数,则称这三个数为“老根数”,其结果中最小的整数称为“最小算术平方根”,最大的整数称为“最大算术平方根”。例如：1,4,9 这三个数,$\sqrt{1× 4}= 2$,$\sqrt{1× 9}= 3$,$\sqrt{4× 9}= 6$,其结果分别为 2,3,6,都是整数,所以 1,4,9 这三个数称为“老根数”,其中“最小算术平方根”是 2,“最大算术平方根”是 6。
(1)试说明：2,8,50 这三个数是“老根数”,并求出其“最小算术平方根”与“最大算术平方根”；
(2)已知 16,$a$,36 这三个数是“老根数”,且其“最大算术平方根”是“最小算术平方根”的 2 倍,求$a$的值。

答案： 9.【解】
(1)因为$\sqrt{2×8}=4$，$\sqrt{2×50}=10$，$\sqrt{8×50}=20$，所以2，8，50这三个数是“老根数”，其中“最小算术平方根”是4， “最大算术平方根”是20。
(2)当a＜16时，$2\sqrt{a×16}=\sqrt{16×36}$，解得a =9;当16＜a＜36时，$2\sqrt{16a}=\sqrt{36a}$，解得a=0，不合题意，舍去；当a＞36时，$2\sqrt{16×36}=\sqrt{36a}$，解得a=64。综上所述，a的值为9或64。