《2025年初中必刷题八年级数学上册华师大版》

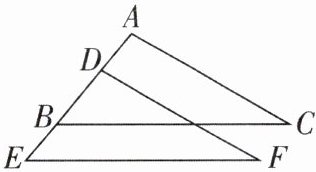
1[中]如图,点A,D,B,E在一条直线上,$AC// DF$,$BC// EF$,$AC= DF$,试说明$AD= BE$。

答案： 因为AC//DF，BC//EF，所以∠A = ∠EDF，∠ABC = ∠E。又因为AC = DF，所以△ABC≌△DEF(AAS)，所以AB = DE，则AB - BD = DE - BD，所以AD = BE。

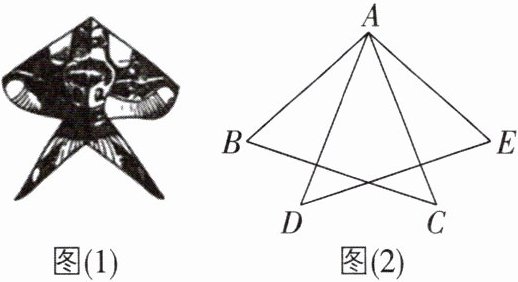
2[中]如图(1)是小军制作的燕子风筝,燕子风筝的骨架图如图(2)所示,$AB= AE$,$AC= AD$,$∠BAD= ∠EAC$,$∠C= 50^{\circ}$,求$∠D$的大小。

答案： 因为∠BAD = ∠EAC，所以∠BAD + ∠CAD = ∠EAC + ∠CAD，即∠BAC = ∠EAD。在△BAC与△EAD中，AB = AE，∠BAC = ∠EAD，AC = AD，所以△BAC≌△EAD(SAS)，所以∠D = ∠C = 50°。

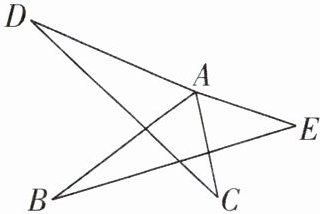
3[2024江苏淮安调研,中]如图,已知$AD= AB$,$AC= AE$,$∠DAB= ∠CAE$,连结DC,BE。
(1)试说明：$\triangle BAE\cong \triangle DAC$。
(2)若$∠CAD= 125^{\circ}$,$∠D= 20^{\circ}$,求$∠E$的度数。

答案：
(1)因为∠DAB = ∠CAE，所以∠DAB + ∠BAC = ∠CAE + ∠BAC，所以∠DAC = ∠BAE。又因为AD = AB$,$AC = AE，所以△BAE≌△DAC(SAS)。
(2)因为△BAE≌△DAC，所以∠E = ∠C。因为∠CAD = 125°，∠D = 20°，所以∠C = 180° - (∠CAD + ∠D)=180° - (125° + 20°)=35°，所以∠E = ∠C = 35°。

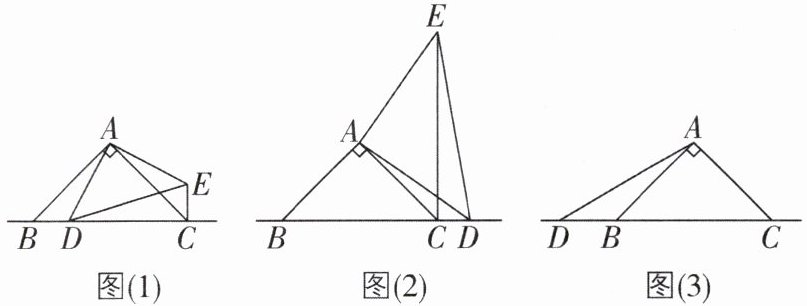
4[2025江西赣州质检,中]已知在$\triangle ABC和\triangle ADE$中,$∠BAC= ∠DAE= 90^{\circ}$,$AB= AC$,$AD= AE$,点D是直线BC上的一动点(点D不与点B,C重合),连结CE。
(1)如图(1),当点D在边BC上时,求证：$BC= CE+CD$。(提示：证全等)
(2)如图(2),当点D在边BC的延长线上时,结论$BC= CE+CD$是否成立？若成立,请进行证明；若不成立,请猜想BC,CE,CD之间存在的数量关系。猜想CE与BC的位置关系,并说明理由。
(3)如图(3),当点D在边BC的反向延长线上时,补全图形,不需要写证明过程,直接写出BC,CE,CD之间存在的数量关系。

答案：
(1)【证明】
∵ ∠BAC = ∠DAE = 90°，
∴∠BAD + ∠DAC = ∠CAE + ∠DAC，
∴∠BAD = ∠CAE。又
∵AB = AC，AD = AE，
∴△ABD≌△ACE(SAS)，
∴BD = CE，
∴BD + CD = CE + CD。
(2)【解】不成立，存在的数量关系为CE = BC + CD，位置关系为CE⊥BC，理由如下:
∵∠BAC = ∠DAE = 90°，
∴∠BAD = ∠CAE。又
∵AB = AC，AD = AE，
∴△ABD≌△ACE (SAS)，
∴BD = CE，∠ACE = ∠ABD。
∵BD = BC + CD，
∴CE = BC + CD。
∵∠BAC = 90°，AB = AC，
∴ ∠ABC = ∠ACB = 45°，
∴∠ACE = ∠ABD = 45°，
∴∠BCE = 45° + 45° = 90°，
∴CE⊥BC。
(3)补全图形如图所示。存在的数量关系为CD = BC + CE。理由如下:如图，
∵∠BAC = ∠DAE = 90°，
∴∠BAD = ∠CAE。又
∵AB = AC，AD = AE，
∴△ABD≌△ACE(SAS)，
∴BD = CE，
∴CD = BC + BD = BC + CE。

5[中]如图,在$\triangle ABC$中,$AB= AC= 9$,点E在边AC上,点D在边BC上,且$AD= DE$,若$∠ADE= ∠B$,$CD= 3BD$,求CE的长。

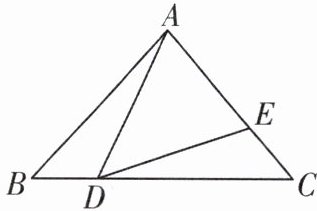
答案：
∵AB = AC，
∴∠B = ∠C。
∵∠ADE = ∠B，∠BAD = 180° - ∠B - ∠ADB，∠CDE = 180° - ∠ADE - ∠ADB，
∴∠BAD = ∠CDE。在△ABD与△DCE中，∠BAD = ∠CDE，∠B = ∠C，AD = DE，所以△ABD≌△DCE(AAS)，所以CD = AB = 9，BD = CE。
∵CD = 3BD，
∴CE = BD = 3。