《2025年初中必刷题八年级数学上册华师大版》

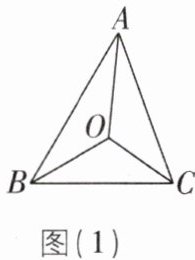
1 [2024河北保定期末,中]如图(1),把△ABC剪成三部分,将边AB,BC,AC放在同一直线l上,点O都落在直线MN上,直线MN // l,如图(2)所示。在△ABC中,若∠BOC = 115°,则∠BAC的度数为( )



A.50°
B.60°
C.65°
D.70°

答案：
1.A　[解析]如图,过点O,O',O''分别作OD⊥AB于D,O'E⊥BC于E,O''F⊥CA'于F.
∵直线MN//l,
∴OD=O'E=O''F,
∴点O为△ABC三条内角平分线的交点，
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=2(180°−∠BOC)=2(∠180°−115°)=130°,
∴∠BAC=50°.故选A.

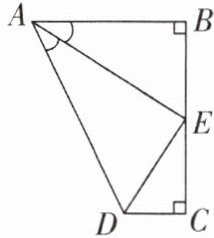
2 [中]如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD。下列结论：①∠AED = 90°；②∠ADE = ∠CDE；③DE = BE；④AD = AB + CD。其中成立的是( )

A.①③
B.①②③
C.②④
D.①②④

答案：
2.D　[解析]过E作EF⊥AD于F,如图.
∵AB⊥BC,AE平分∠BAD,
∴BE=EF,
∴易证Rt△AEF≌Rt△AEB,
∴AF=AB,∠AEF=∠AEB.
∵E是BC的中点，
∴EC=BE=EF,故③错误;
∵易证Rt△EFD≌Rt△ECD,
∴DF=DC,∠FDE=∠CDE,∠FED=∠CED,故②正确;
∴AD=AF+FD=AB+DC,故④正确;
∴∠AED=∠AEF+∠FED=$\frac{1}{2}$∠BEC=90°,故①正确.故选D.

3 [2025内蒙古呼和浩特质检,较难]如图,在Rt△ABC中,∠ACB = 90°,∠BAC的平分线交BC于点D,过点C作CG⊥AB于点G,交AD于点E,过点D作DF⊥AB于点F。下列结论中一定正确的是( )
①∠CED = ∠CDE；②S_{△AEC} : S_{△AEG} = AC : AG；③∠ADF = ∠FDB；④CE = DF。

A.①②③④
B.①②
C.①②③
D.①②④

答案：
3.D　[解析]
∵∠ACB=90°,
∴∠CAD+∠CDE=90°.
∵CG⊥AB,
∴∠EGA=90°,
∴∠EAG+∠AEG=90°,
∴∠CAD+∠CDE=∠EAG+∠AEG=90°.
∵AD平分∠BAC,
∴∠CAD=∠EAG,
∴∠CDE=∠AEG.
又
∵∠AEG=∠CED,
∴∠CED=∠CDE,故结论①正确.
如图，过点E作EH⊥AC于H.
∵AD平分∠BAC,EG⊥AB,
∴EG=EH.
∵S△AEC=$\frac{1}{2}$·AC·EH,S△AEG=$\frac{1}{2}$·AG·EG,
∴S△AEC:S△AEG=($\frac{1}{2}$·AC·EH):($\frac{1}{2}$·AG·EG)=AC:AG,故结论②正确.
∵DF⊥AB,
∴∠DFA=90°.又
∵∠DCA=90°,
∴∠DCA=∠DFA.
在△CAD和△FAD中,
∵{∠DCA=∠DFA,∠CAD=∠FAD,AD=AD},
∴△CAD≌△FAD(AAS),
∴∠ADC=∠ADF.
∵∠ADC+∠ADF+∠FDB=180°,
∴2∠ADF+∠FDB=180°,无法证明∠FDB=180°−2∠ADF.根据已知条件无法证明∠ADF=∠FDB,故结论③不一定正确.
∵∠CED=∠CDE,
∴CE=CD.
∵△CAD≌△FAD,
∴CD=DF,
∴CE=DF,故结论④正确.
综上所述，正确的有①②④，故选D.

4 [中]如图,在△ABC中,∠C = 90°,AC = BC。以点A为圆心,任意长为半径作弧交AB,AC于D,E两点；分别以点D,E为圆心,大于$\frac{1}{2}DE$长为半径作弧,在∠BAC内两弧相交于点P；作射线AP交BC于点F,过点F作FG⊥AB,垂足为G。若AB = 8 cm,则△BFG的周长等于______cm。

答案：
4.8
[解析]在△ABC中，
∵∠C=90°,
∴FC⊥AC.
由作图方法可得AF平分∠BAC.
∵FG⊥AB,
∴∠BAF=∠CAF,FC=FG.
在Rt△ACF和Rt△AGF中,
∵{AF=AF,FC=FG},
∴Rt△ACF≌Rt△AGF (HL),
∴AC=AG.
∵AC=BC,
∴AG=BC,
∴△BFG的周长为GF+BF+BG=CF+BF+BG=BC+BG=AG+BG=AB=8cm.故答案为8.

5 [2025四川达州期末,中]如图,△ABC的外角∠MBC和∠NCB的平分线BP,CP相交于点P,PE⊥BC于E,且PE = 3 cm,若△ABC的周长为$15 cm,S_{△BPC} = 7.5 cm^2,$则△ABC的面积为$______cm^2。$

答案：
5.7.5　[解析]如图，过点P作PF⊥AN于F,作PG⊥AM于G,连结AP.
∵∠GBC和∠FCB的平分线BP,CP相交于点P,PE⊥BC,
∴PF=PG=PE=3cm.
∵S△BPC=7.5cm²,
∴$\frac{1}{2}$BC·PE=7.5cm²,
∴BC=5cm.
∵△ABC的周长为15cm,
思路分析：根据直角三角形的性质，角平分线的定义，可证明∠CED=∠CDE；过点E作EH⊥AC于H，根据角平分线的性质EG=EH,再利用三角形的面积公式即可证得S△AEC:S△AEG=AC:AG；根据题目给定的条件，无法证明∠FDB；由结论①正确可证△CAD≌△FAD可得CD=DF,则CE=DF。
刷有所得：求三角形面积时要认真分析图形，根据三角形的面积公式找到一个底边和此底边上对应的高即可。
∴AB+AC+BC=15cm,
∴AB+AC=10cm,
∴S△ABC=S△ACP+S△ABP−S△BCP=$\frac{1}{2}$AC·PF+$\frac{1}{2}$AB·PG−$\frac{1}{2}$BC·PE=$\frac{1}{2}$(AC+AB−BC)×3=$\frac{1}{2}$×(10−5)×3=7.5(cm²).故答案为7.5.

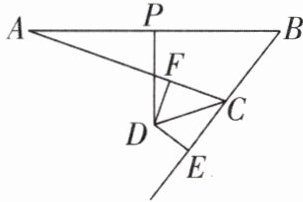
6 [2024河北沧州期末,中]如图,CD是∠ACE的平分线,DP垂直平分AB于点P,DF⊥AC于点F,DE⊥BC于点E。
(1)求证：AF = BE；
(2)若BC = 3 cm,AC = 5 cm,则CE = ______。

答案： 6.
(1)[证明]连结AD,BD.
∵PD垂直平分AB,
∴AD=BD.
∵CD平分∠ACE,DE⊥BC,DF⊥AC,
∴DE=DF,∠AFD=∠BED=90°.
在Rt△ADF和Rt△BDE中,
∵{AD=BD,DF=DE},
∴Rt△ADF≌Rt△BDE(HL),
∴AF=BE.
(2)[解]设CE=CF=x,则AF=AC−CF=5−x,BE=BC+CE=3+x.
∵AF=BE,
∴5−x=3+x,
∴x=1,
∴CE=1cm.
故答案为1cm.

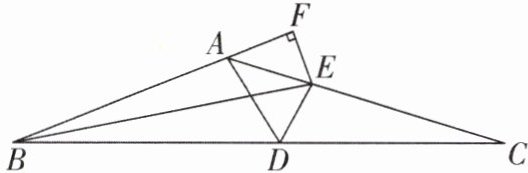
7 [难]如图,△ABC中,点D在BC边上,∠BAD = 100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,交BA的延长线于点F,且∠AEF = 50°,连结DE。
(1)求∠CAD的度数；
(2)求证：DE平分∠ADC；
(3)若AB = 7,AD = 4,CD = 8,且S_{△ACD} = 15,求△ABE的面积。

答案：
7.
(1)[解]
∵EF⊥AB,∠AEF=50°,
∴∠FAE=90°−50°=40°.
∵∠BAD=100°,
∴∠CAD=180°−100°−40°=40°.
(2)[证明]如图,过点E作EG⊥AD于G,EH⊥BC于H.
∵∠FAE=∠DAE=40°,EF⊥BF,EG⊥AD,
∴EF=EG.
∵BE平分∠ABC,EF⊥BF,EH⊥BC,
∴EF=EH,
∴EG=EH,
∴DE平分∠ADC.
(3)[解]
∵S△ACD=15,
∴$\frac{1}{2}$×AD×EG+$\frac{1}{2}$×CD×EH=15,即$\frac{1}{2}$×4×EG+$\frac{1}{2}$×8×EH=15,
解得EG=EH=$\frac{5}{2}$,
∴EF=EH=$\frac{5}{2}$.
∴△ABE的面积为$\frac{1}{2}$×AB×EF=$\frac{1}{2}$×7×$\frac{5}{2}$=$\frac{35}{4}$.