《2025年初中必刷题八年级数学上册华师大版》

1 [2025 山西太原期中]如图,已知$\triangle ABD和\triangle ACD关于直线AD$成轴对称,$\angle B = 30^{\circ}$,$\angle BAC = 62^{\circ}$,则$\angle BDC$的度数为( )

A.$122^{\circ}$
B.$124^{\circ}$
C.$138^{\circ}$
D.$150^{\circ}$

答案： 1.A [解析]
∵△ABD和△ACD关于直线AD成轴对称,∠B = 30°,∠BAC = 62°,
∴△ABD≌△ACD,
∴∠BAD = ∠CAD = $\frac{1}{2}$∠BAC = 31°,
∴∠BDA = 180° - ∠B - ∠BAD = 119°,
思路分析：由旋转的性质得到△ABC≌△ADE,得到$S_{\triangle ABC}=S_{\triangle ADE}=S_{\triangle AEF}+S_{\triangle DEF}$,由$S_{\triangle ACF}-S_{\triangle DEF}=\frac{5}{2}S_{\triangle ABC}$得到$S_{\triangle ACF}+S_{\triangle ABC}-S_{\triangle DEF}=\frac{5}{2}S_{\triangle ABC}+S_{\triangle ABC}$,进一步求得$S_{\triangle ACE}=\frac{7}{2}S_{\triangle ABC}$,作AH⊥BE于点H,由三角形面积公式即可求得$\frac{BC}{CE}$的值。
思路分析：由D为BC中点知BD = 3,再由折叠性质得ND = NA,从而根据△DNB的周长为ND + NB + BD = NA + NB + BD = AB + BD可得答案。
∴∠CDA = ∠BDA = 119°,
∴∠BDC = 360° - ∠BDA - ∠CDA = 122°.故选A.

2 [2025 辽宁辽阳期中]如图,$\triangle ABC沿边BC所在直线向右平移得到\triangle DEF$,则下列结论不一定正确的是( )

A.$\triangle ABC \cong \triangle DEF$
B.$\angle A = \angle D$
C.$AB // DE$
D.$EC = FC$

答案： 2.D [解析]根据平移的特征可得，△ABC≌△DEF,∠A = ∠D,AB//DE,故A、B、C正确,不符合题意;EC与FC不一定相等，故D不一定正确，符合题意.故选D.

3 [2025 四川宜宾期末]如图,$M在BC$上,$MB = \frac{1}{2}MC$,如果$\triangle ABC绕点M按顺时针方向旋转180^{\circ}后与\triangle FED$重合,则以下结论中不正确的是( )

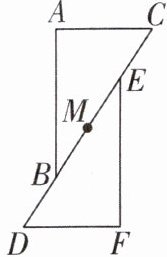
A.$\triangle ABC和\triangle FED$的面积相等
B.$\triangle ABC和\triangle FED$的周长相等
C.$\angle A + \angle ABC = \angle F + \angle FDE$
D.$AC // DF$,且$AC = DF$

答案： 3.C [解析]
∵△ABC绕点M按顺时针方向旋转180°后与△FED重合，
∴△ABC≌△FED,
∴△ABC和△FED的面积相等，△ABC和△FED的周长相等,∠A = ∠F,∠ABC = ∠FED,∠C = ∠D,AC = DF,
∴AC//DF,∠A + ∠ABC = ∠F + ∠FED,故A、B、D正确,C不正确.故选C.

4 [2025 山东青岛期中]如图,将$\triangle ABC绕点A按逆时针方向旋转得到\triangle ADE$,点$C的对应点E恰好落在边BC$的延长线上,$AD与BE相交于点F$,则图中全等的三角形为______,$\angle BAC$的对应角为______,$DE$的对应边为______。若$S_{\triangle ACF} - S_{\triangle DEF} = \frac{5}{2}S_{\triangle ABC}$,则$\frac{BC}{CE} = $______。

答案：
4.△ABC≌△ADE ∠DAE BC $\frac{2}{7}$ [解析]
∵把△ABC绕点A按逆时针方向旋转得到△ADE,
∴△ABC≌△ADE,
∴∠BAC = ∠DAE,DE = BC,
∴$S_{\triangle ABC}=S_{\triangle ADE}=S_{\triangle AEF}+S_{\triangle DEF}$.
∵$S_{\triangle ACF}-S_{\triangle DEF}=\frac{5}{2}S_{\triangle ABC}$,
∴$S_{\triangle ACF}+S_{\triangle ABC}-S_{\triangle DEF}=\frac{5}{2}S_{\triangle ABC}+S_{\triangle ABC}$,
∴$S_{\triangle ACF}+S_{\triangle AEF}+S_{\triangle DEF}-S_{\triangle DEF}=\frac{5}{2}S_{\triangle ABC}+S_{\triangle ABC}$,
∴$S_{\triangle ACF}+S_{\triangle AEF}=\frac{7}{2}S_{\triangle ABC}$,即$S_{\triangle ACE}=\frac{7}{2}S_{\triangle ABC}$.作AH⊥BE于点H,如图所示,则$\frac{1}{2}CE\cdot AH=\frac{7}{2}×\frac{1}{2}BC\cdot AH$,
∴2CE = 7BC,
∴$\frac{BC}{CE}=\frac{2}{7}$.故答案为△ABC≌△ADE,∠DAE,BC,$\frac{2}{7}$.

5 如图,将$\triangle ABC$折叠,使点$A与BC边的中点D$重合,折痕为$MN$,若$AB = 9$,$BC = 6$,则$\triangle DNB$的周长为______。

答案： 5.12 [解析]由折叠的性质可知,△AMN≌△DMN,
∴AN = DN.
∵D为BC的中点，且BC = 6,
∴BD = $\frac{1}{2}$BC = 3,
∴△DNB的周长为ND + NB + BD = NA + NB + BD = AB + BD = 9 + 3 = 12.故答案为12.

6 [2025 新疆乌鲁木齐期中]如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿$BC方向平移到\triangle DEF$的位置,若$AB = 8.5$,$DO = 2$,平移距离为$4$,则阴影部分面积为______。

答案： 6.30 [解析]由平移的性质得△ABC≌△DEF,BE = 4,DE = AB = 8.5,AB//DE,
∴$S_{\triangle ABC}=S_{\triangle DEF}$,OE = DE - DO = 8.5 - 2 = 6.5,∠ABC = ∠DEF = 90°,
∴$S_{阴影}=S_{\triangle DEF}-S_{\triangle OEC}=S_{\triangle ABC}-S_{\triangle OEC}=S_{梯形ABEO}=\frac{1}{2}(6.5 + 8.5)×4 = 30$.故答案为30.

7 新考向传统文化[2025 湖北武汉期中]中国古代数学家刘徽在《九章算术注》中,给出证明三角形面积公式的出入相补法。如图所示,在$\triangle ABC$中,分别取$AB$,$AC的中点D$,$E$,连结$DE$,过点$A作AF \perp DE$,垂足为$F$,将$\triangle ABC分割后拼接成长方形BCHG$。已知$DE = 6$,$AF = 3$,则$\triangle ABC$的面积为______。

答案： 7.36 [解析]由题意可知△ADF≌△BDG,于是可得△AEF≌△CEH,
∴AF = BG,DF = DG,AF = CH,EF = EH,△ABC的面积 = 四边形BCHG的面积,
∴BG = CH = AF = 3,GH = DG + DF + EF + EH = 2DE = 12.
∵四边形BCHG是长方形,
∴$S_{\triangle ABC}=S_{长方形BCHG}=GH\cdot BG = 12×3 = 36$,故答案为36.

8 [2025 湖南怀化期末]根据下列条件,能画出唯一的$\triangle ABC$的是( )

A.$AB = 3$,$BC = 4$
B.$BC = 8\ cm$,$\angle A = 60^{\circ}$
C.$\angle A = 60^{\circ}$,$\angle B = 45^{\circ}$
D.以上都不对

答案： 8.D [解析]A选项,由AB = 3,BC = 4,不能画出唯一的△ABC;B选项,由BC = 8cm,∠A = 60°,不能画出唯一的△ABC;C选项，由∠A = 60°,∠B = 45°不能画出唯一的△ABC.故选D.

9 下列说法正确的是( )

A.两个面积相等的图形一定是全等图形
B.两个等边三角形是全等三角形
C.两个能够互相重合的三角形是全等三角形
D.若两个图形的周长相等,则它们一定是全等图形

答案： 9.C [解析]A长为8,宽为2的长方形的面积等于边长为 的正方形的面积,但它们不是全等图形,故A不符合题意。B边长为 的等边三角形和边长为 的等边三角形并不全等,故B不符合题意。C
∵能够互相重合的图形是全等图形,
∴能够互相重合的三角形是全等三角形,故C符合题意。D边长分别为 的三角形的周长等于边长为 的正方形的周长,但它们不是全等图形,故D不符合题意。