第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2024 河北邢台期末,中]篮子里有若干个苹果,可以平均分给$(x + 1)$名同学,也可以平均分给$(x - 3)$名同学($x为大于3$的正整数),用代数式表示苹果数量不可能的是( )
A.$(x + 1)(x - 3)$
B.$x(x^{2}-2x - 3)$
C.$x^{2}-4x + 3$
D.$2x^{3}-4x^{2}-6x$
A.$(x + 1)(x - 3)$
B.$x(x^{2}-2x - 3)$
C.$x^{2}-4x + 3$
D.$2x^{3}-4x^{2}-6x$
答案:
C 【解析】A 选项,(x+1)(x-3)能分别被(x+1),(x-3)整除,故 A 选项不符合题意;B 选项,x(x²-2x-3)=x(x+1)(x-3),能分别被(x+1),(x-3)整除,故 B 选项不符合题意;C 选项,x²-4x+3=(x-1)(x-3),不能被(x+1)整除,故 C 选项符合题意;D 选项,2x³-4x²-6x=2x(x²-2x-3)=2x(x+1)(x-3),能分别被(x+1),(x-3)整除,故 D 选项不符合题意.故选 C.
2 [中]若$A = x^{2}+2x - 6y$,$B = -y^{2}+4x - 11$,则$A$,$B$的大小关系为( )
A.$A>B$
B.$A<B$
C.$A\geqslant B$
D.$A = B$
A.$A>B$
B.$A<B$
C.$A\geqslant B$
D.$A = B$
答案:
A 【解析】A-B=x²+2x-6y-(-y²+4x-11)=x²+2x-6y+y²-4x+11=x²-2x+y²-6y+11=x²-2x+1+y²-6y+9+1=(x-1)²+(y-3)²+1.
∵(x-1)²≥0,(y-3)²≥0,
∴(x-1)²+(y-3)²+1≥1,即A-B≥1,
∴A>B.故选 A.
∵(x-1)²≥0,(y-3)²≥0,
∴(x-1)²+(y-3)²+1≥1,即A-B≥1,
∴A>B.故选 A.
3 [中]分解因式$x^{2}+ax + b$,甲看错了$a$的值,分解的结果为$(x + 6)(x - 1)$,乙看错了$b$的值,分解的结果为$(x - 2)(x + 1)$,那么$x^{2}+ax + b$分解的正确结果为( )
A.$(x - 2)(x + 3)$
B.$(x + 2)(x - 3)$
C.$(x - 2)(x - 3)$
D.$(x + 2)(x + 3)$
A.$(x - 2)(x + 3)$
B.$(x + 2)(x - 3)$
C.$(x - 2)(x - 3)$
D.$(x + 2)(x + 3)$
答案:
B 【解析】(x+6)(x-1)=x²+5x-6,(x-2)(x+1)=x²-x-2.因为甲看错了a的值而没有看错b的值,所以b=-6.因为乙看错了b的值而没有看错a的值,所以a=-1,所以多项式x²+ax+b为x²-x-6=(x-3)(x+2).故选 B.
4 [2025 山东烟台期中,中]$2^{48}-1能被60到70$之间的某两个整数整除,则这两个数是( )
A.$61和63$
B.$63和65$
C.$65和67$
D.$64和67$
A.$61和63$
B.$63和65$
C.$65和67$
D.$64和67$
答案:
B 【解析】2⁴⁸-1=(2²⁴+1)(2²⁴-1)=(2²⁴+1)(2¹²+1)(2¹²-1)=(2²⁴+1)(2¹²+1)(2⁶+1)(2⁶-1)=(2²⁴+1)(2¹²+1)×65×63,故选 B.
5 [中]已知$x\neq y$,且满足两个等式$x^{2}-2y = 2021^{2}$,$y^{2}-2x = 2021^{2}$,则$x^{2}+2xy + y^{2}$的值为____。
答案:
4 【解析】{x²-2y=2021,①y²-2x=2021,②①-②,得x²-y²+2x-2y=0,(x+y)(x-y)+2(x-y)=0,(x-y)(x+y+2)=0.
∵x≠y,
∴x+y+2=0,
∴x+y=-2,
∴x²+2xy+y²=(x+y)²=4.故答案为 4.
∵x≠y,
∴x+y+2=0,
∴x+y=-2,
∴x²+2xy+y²=(x+y)²=4.故答案为 4.
6 [2024 广西南宁期中,中]已知$1 + x + x^{2}= 0$,则$x^{2024}+x^{2023}+x^{2022}+…+x + 1$的值为____。
答案:
0 【解析】
∵1+x+x²=0,
∴x²⁰²⁴+x²⁰²³+x²⁰²²+…+x+1=1+x+x²+x³+x⁴+x⁵+…+x²⁰²²+x²⁰²³+x²⁰²⁴=(1+x+x²)+x³(1+x+x²)+x⁶(1+x+x²)+…+x²⁰²²(1+x+x²)=(1+x+x²)(1+x³+x⁶+…+x²⁰²²)=0.
∵1+x+x²=0,
∴x²⁰²⁴+x²⁰²³+x²⁰²²+…+x+1=1+x+x²+x³+x⁴+x⁵+…+x²⁰²²+x²⁰²³+x²⁰²⁴=(1+x+x²)+x³(1+x+x²)+x⁶(1+x+x²)+…+x²⁰²²(1+x+x²)=(1+x+x²)(1+x³+x⁶+…+x²⁰²²)=0.
7 [中]先阅读下列材料,再解答问题。
材料:因式分解:$(x + y)^{2}+2(x + y)+1$。
解:将$x + y$看成整体,设$x + y = m$,则原式$=m^{2}+2m + 1= (m + 1)^{2}$。
再将$x + y = m$代入,得原式$=(x + y + 1)^{2}$。
上述解题过程用到的是整体思想,整体思想是数学解题过程中常用的一种思想方法。请你写出下列因式分解的结果:
(1)$1 - 2(x - y)+(x - y)^{2}= $____。
(2)$25(a - 1)^{2}-10(a - 1)+1= $____。
(3)$(y^{2}-4y)(y^{2}-4y + 8)+16= $____。
材料:因式分解:$(x + y)^{2}+2(x + y)+1$。
解:将$x + y$看成整体,设$x + y = m$,则原式$=m^{2}+2m + 1= (m + 1)^{2}$。
再将$x + y = m$代入,得原式$=(x + y + 1)^{2}$。
上述解题过程用到的是整体思想,整体思想是数学解题过程中常用的一种思想方法。请你写出下列因式分解的结果:
(1)$1 - 2(x - y)+(x - y)^{2}= $____。
(2)$25(a - 1)^{2}-10(a - 1)+1= $____。
(3)$(y^{2}-4y)(y^{2}-4y + 8)+16= $____。
答案:
(1)(1-x+y)²
(2)(5a-6)²
(3)(y-2)⁴【解析】
(1)设x-y=a,则原式=1-2a+a²=(1-a)².将x-y=a代入,得原式=(1-x+y)².
(2)设a-1=m,则原式=25m²-10m+1=(5m-1)².将a-1=m代入,得原式=(5a-6)².
(3)设y²-4y=a,则原式=a(a+8)+16=a²+8a+16=(a+4)².将y²-4y=a代入,得原式=(y²-4y+4)²=(y-2)⁴.
(1)(1-x+y)²
(2)(5a-6)²
(3)(y-2)⁴【解析】
(1)设x-y=a,则原式=1-2a+a²=(1-a)².将x-y=a代入,得原式=(1-x+y)².
(2)设a-1=m,则原式=25m²-10m+1=(5m-1)².将a-1=m代入,得原式=(5a-6)².
(3)设y²-4y=a,则原式=a(a+8)+16=a²+8a+16=(a+4)².将y²-4y=a代入,得原式=(y²-4y+4)²=(y-2)⁴.
8 [2025 浙江绍兴期中,中]【阅读理解】如何将形如$x^{2}+(p + q)x + pq$的式子分解因式呢?我们知道$(x + p)(x + q)= x^{2}+(p + q)x + pq$,根据因式分解与整式乘法是互逆变形,可得$x^{2}+(p + q)x + pq= (x + p)(x + q)$。例如:$\because(x + 1)(x + 2)= x^{2}+3x + 2$,$\therefore x^{2}+3x + 2= (x + 1)(x + 2)$。上述过程还可以形象地用十字相乘的形式表示:如图,先分解二次项系数,分别写在十字交叉线的左上角和左下角,再分解常数项,分别写在十字交叉线的右上角和右下角,然后交叉相乘再求和,使其等于一次项的系数,这样我们可以得到$x^{2}+3x + 2= (x + 1)(x + 2)$。
【迁移运用】利用上述十字相乘法,将下列多项式分解因式:
(1) 二次项系数为$1$
①$x^{2}+7x + 12$;②$x^{2}+5x + 6$。
(2) 二次项系数不为$1$
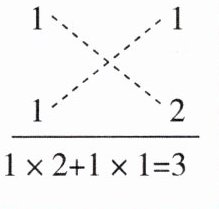
$4x^{2}-5x - 6$。
【迁移运用】利用上述十字相乘法,将下列多项式分解因式:
(1) 二次项系数为$1$
①$x^{2}+7x + 12$;②$x^{2}+5x + 6$。
(2) 二次项系数不为$1$
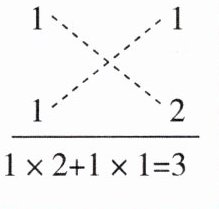
$4x^{2}-5x - 6$。
答案:
【解】
(1)①x²+7x+12=(x+3)(x+4).
②x²+5x+6=(x+2)(x+3).
(2)4x²-5x-6=(4x+3)(x-2).
(1)①x²+7x+12=(x+3)(x+4).
②x²+5x+6=(x+2)(x+3).
(2)4x²-5x-6=(4x+3)(x-2).
9 核心素养运算能力[2025 河南洛阳期中,较难]如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“奇特数”。例如:$8 = 3^{2}-1^{2}$,$16 = 5^{2}-3^{2}$,$24 = 7^{2}-5^{2}$,则$8$,$16$,$24$这三个数都是“奇特数”。
(1)填空:$32$____“奇特数”,$2018$____“奇特数”。(填“是”或者“不是”)
(2)设两个连续奇数是$2n - 1和2n + 1$(其中$n$为正整数),由这两个连续奇数构造的“奇特数”是$8$的倍数吗?
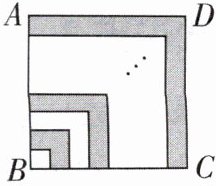
(3)如图所示,拼叠的正方形边长是从$1$开始的连续奇数,按此规律拼叠到正方形$ABCD$,其边长为$403$,求阴影部分的面积。
(1)填空:$32$____“奇特数”,$2018$____“奇特数”。(填“是”或者“不是”)
(2)设两个连续奇数是$2n - 1和2n + 1$(其中$n$为正整数),由这两个连续奇数构造的“奇特数”是$8$的倍数吗?
(3)如图所示,拼叠的正方形边长是从$1$开始的连续奇数,按此规律拼叠到正方形$ABCD$,其边长为$403$,求阴影部分的面积。

答案:
【解】
(1)
∵32=9²-7²,
∴32是“奇特数”.
∵2018不能表示为两个连续奇数的平方差,
∴2018不是“奇特数”.故答案为是,不是.
(2)
∵(2n+1)²-(2n-1)²=(2n+1+2n-1)(2n+1-2n+1)=4n×2=8n,
∴由这两个连续奇数构造的“奇特数”是8的倍数.
(3)由题意得S阴影部分=3²-1²+7²-5²+11²-9²+…+403²-401²=(3-1)(3+1)+(7-5)(7+5)+(11-9)(11+9)+…+(403-401)(403+401)=2×(1+403)×2022=81608.
(1)
∵32=9²-7²,
∴32是“奇特数”.
∵2018不能表示为两个连续奇数的平方差,
∴2018不是“奇特数”.故答案为是,不是.
(2)
∵(2n+1)²-(2n-1)²=(2n+1+2n-1)(2n+1-2n+1)=4n×2=8n,
∴由这两个连续奇数构造的“奇特数”是8的倍数.
(3)由题意得S阴影部分=3²-1²+7²-5²+11²-9²+…+403²-401²=(3-1)(3+1)+(7-5)(7+5)+(11-9)(11+9)+…+(403-401)(403+401)=2×(1+403)×2022=81608.
查看更多完整答案,请扫码查看


