《2025年初中必刷题八年级数学上册华师大版》

1 [2025河南焦作期中,中]如图,D为等腰三角形ABC内一点,$AC = BC = BP$,$AD = BD$,$\angle DBP = \angle DBC$,$\angle C = 62^{\circ}$,则$\angle BPD$的度数为( )

A.$20^{\circ}$
B.$28^{\circ}$
C.$30^{\circ}$
D.$31^{\circ}$

答案：
D 【解析】连结CD,如图.
在△BCD和△ACD中，
{BD=AD,CD=CD,BC=AC,
∴ △BCD≌△ACD(SSS),
∴ ∠BCD=∠ACD=$\frac{1}{2}$∠ACB=31°.在△BCD和△BPD中，{BD=BD,∠CBD=∠PBD,BC=BP,
∴ △BCD≌△BPD,
∴ ∠BCD=∠BPD=31°,
故选D.

2 [中]如图,在$\triangle ABC$中,E,D分别是边AB,AC上的点,且$AE = AD$,BD,CE交于点F,AF的延长线交BC于点H。若$\angle EAF = \angle DAF$,则图中的全等三角形共有( )

A.4对
B.5对
C.6对
D.7对

答案： D 【解析】在△AEF和△ADF中，{AE=AD,∠EAF=∠DAF,AF=AF,所以△AEF≌△ADF(SAS),所以EF=DF,∠EFA=∠DFA,所以∠FDC=∠FEB.在△EBF和△DCF中，{∠EFB=∠DFC,EF=DF,∠FEB=∠FDC,
所以△EBF≌△DCF(ASA),所以BF=CF,
∠EBF=∠DCF,所以∠HFC=∠HFB.在△HFC和△HFB中，{FC=FB,∠HFC=∠HFB,FH=FH,所以
△HFC≌△HFB(SAS).在△ABF和△ACF中，{AB=AC,AF=AF,FB=FC,所以△ABF≌△ACF(SSS),同理可得△ABH≌△ACH(SSS),△BEC≌△CDB(SSS),△ABD≌△ACE(SSS).故选D.

3 [新考法][2025山西晋城期中,较难]如图,已知$AB = AC$,AD为$\angle BAC$的平分线,D,E,F,…为$\angle BAC$的平分线上的点。如图(1),连结BD,CD；如图(2),连结BD,CD,BE,CE；如图(3),连结BD,CD,BE,CE,BF,CF；…,以此规律,第2025个图形中全等三角形的对数是( )
A. 2049300
B. 2051325
C. 2068224
D. 2084520

答案： B 【解析】题图
(1)中，
∵ AD为∠BAC的平分线，
∴ ∠BAD=∠CAD.在△ABD和△ACD中，{AB=AC,∠BAD=∠CAD,AD=AD,
∴ △ABD≌△ACD(SAS),
∴ 共$\frac{1×2}{2}$ = 1(对)全等三角形.同理,题图
(2)中，△ABD≌△ACD,△ABE≌△ACE,
∴ BD=CD,BE=CE.在△BDE和△CDE中，
{BD=CD,BE=CE,DE=DE,
∴ △BDE≌△CDE(SSS),
∴ 共$\frac{2×3}{2}$ = 3(对)全等三角形.同理,题图
(3)中，
△ABD≌△ACD,△ABE≌△ACE,△BDE≌△CDE,△BEF≌△CEF,△BDF≌△CDF,
△ABF≌△ACF,共有$\frac{3×4}{2}$ = 6(对)全等三角形.由此发现，第n(n为正整数)个图形中，全等三角形有$\frac{n(n + 1)}{2}$对.
关键点拨：巧用三角形全等的判定定理是解题的关键.
关键点拨：本题的解题关键是根据题中三个图形中全等三角形的对数得出规律，灵活运用多种三角形全等的判定定理得到边角之间的等量关系是解题的关键.
∴ 第2025个图形中有$\frac{2025×2026}{2}$ = 2051325(对)全等三角形,故选B.

4 [2025吉林长春期末,中]两组邻边分别相等的四边形叫做筝形。如图,四边形ABCD是一个筝形,其中$AD = CD$,$AB = CB$,AC,BD交于点O,得到如下结论：①$AC\perp BD$；②$AO = CO = \frac{1}{2}AC$；③$\triangle ABD\cong\triangle CBD$；④$S_{四边形ABCD} = \frac{1}{2}AC\cdot BD$,其中正确的结论有______(填序号)。

答案： ①②③④ 【解析】在△ABD和△CBD中，
{AD=CD,BD=BD,AB=CB,
∴ △ABD≌△CBD(SSS),故③正确.
∴ ∠ADB=∠CDB.在△AOD和△COD中，
{AD=CD,∠ADO=∠CDO,DO=DO,
∴ △AOD≌△COD(SAS),
∴ AO=CO,∠AOD=∠COD.
∵ AO + CO=AC,
∠AOD + ∠COD=180°,
∴ AO=CO=$\frac{1}{2}$AC,
∠AOD=∠COD=90°,
∴ AC⊥BD,故①②正确.S四边形ABCD=S△ABD+S△CBD=$\frac{1}{2}$BD·OA + $\frac{1}{2}$BD·OC=$\frac{1}{2}$BD·(OA + OC)=$\frac{1}{2}$AC·BD,
故④正确.综上所述,正确的有①②③④,故答案为①②③④.

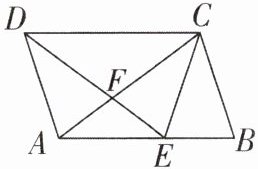
5 [中]如图,已知点E是AB上一点,$AB = DE$,$BC = EC$,$AC = DC$,AC与DE交于点F。
(1)求证：$\angle ACD = \angle BCE$；
(2)若$\angle CEB = \angle CFE$,$\angle ACE = 36^{\circ}$,求$\angle ACB$的度数。

答案：
(1)【证明】
∵ 在△ABC和△DEC中，
{AB=DE,BC=EC,AC=DC,
∴ △ABC≌△DEC(SSS),
∴ ∠ACB=∠DCE,
∴ ∠DCE - ∠ACE=
∠ACB - ∠ACE,
∴ ∠ACD=∠BCE.
(2)【解】
∵ ∠CEB=∠BAC + ∠ACE,∠CFE=
∠EDC + ∠ACD,∠CEB=∠CFE,
∴ ∠BAC +
∠ACE=∠EDC + ∠ACD.由
(1)知,△ABC≌
△DEC,
∴ ∠BAC=∠EDC,
∴ ∠ACE=
∠ACD.
∵ ∠ACE=36°,
∴ ∠DCE=∠ACE +
∠ACD=36° + 36°=72°.由
(1)知,∠ACB=
∠DCE,
∴ ∠ACB=72°.

6 [核心素养·推理能力][2024上海虹口区校级期末,难](1)如图(1),四边形ABCD中,$\angle ABC与\angle ADC$互补,$BC = CD$,点E,F分别在线段AB,AD上,且$BE + DF = EF$。若$\angle A = n^{\circ}$,求$\angle ECF$的度数；
(2)如图(2),若点E,F分别在线段AB,AD的延长线上,其余条件均不变,求$\angle ECF$的度数。

答案：
【解】
(1)如图
(1),延长AD到G,使DG=BE,
连结CG.
∵ ∠ABC+∠ADC=180°,
∴ ∠A+
∠BCD=360°-(∠ABC+∠ADC)=180°.
∵ ∠ADC+∠CDG=180°,
∴ ∠CDG=∠ABC.
∵ BC=CD,DG=BE,
∴ △CBE≌△CDG(SAS),
∴ CE=CG,∠BCE=∠DCG.
∵ BE+DF=EF,DG+DF=FG,
∴ EF=FG.
∵ CF=CF,
∴ △CEF≌△CGF(SSS),
∴ ∠ECF=∠GCF,
∴ ∠ECF=∠GCD+∠DCF=
∠BCE+∠DCF,
∴ ∠ECF=$\frac{1}{2}$∠BCD=
$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$(180°-n°)=90°-$\frac{1}{2}$n°,
∴ ∠ECF的度数为90°-$\frac{1}{2}$n°.

(2)如图
(2),延长DA到G,使DG=BE,连结
CG.
∵ ∠ABC+∠ADC=180°,∠ABC+∠CBE=
180°,
∴ ∠ADC=∠CBE.
∵ BC=CD,DG=BE,
∴ △CBE≌△CDG(SAS),
∴ CE=CG,∠BEC=∠DGC.
∵ BE+DF=EF,DG+DF=FG,
∴ EF=FG.
∵ CF=CF,
∴ △CEF≌△CGF(SSS),
∴ ∠CGF=∠CEF,∠CFE=∠CFG=
$\frac{1}{2}$∠AFE,
∴ ∠BEC=∠CEF=$\frac{1}{2}$∠AEF,
∴ ∠ECF=180°-(∠CEF+∠CFE)=180°-
($\frac{1}{2}$∠AEF+$\frac{1}{2}$∠AFE)=180°-$\frac{1}{2}$(∠AEF+
∠AFE)=180°-$\frac{1}{2}$(180°-∠EAF)=180°-
$\frac{1}{2}$(180°-n°)=180°-90°+$\frac{1}{2}$n°=90°+$\frac{1}{2}$n°,
∴ ∠ECF的度数为90°+$\frac{1}{2}$n°.