《2025年初中必刷题八年级数学上册华师大版》

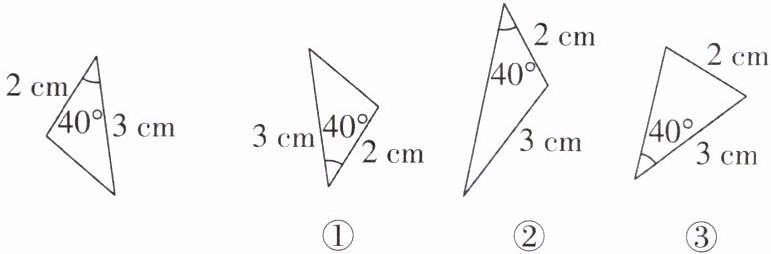
1 [2024 河北廊坊期中]如图，下列与图中三角形全等的是（ ）


A.①②
B.②③
C.①③
D.只有①

答案： 1. D 【解析】由题图可得已知两边及其40°的夹角，只有①与题图满足两边及其夹角分别相等，
∴这两个三角形全等，而②③都不满足条件，故不符合题意，故选D.

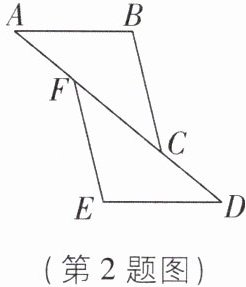
2 [2025 安徽马鞍山期末]如图，已知$BC = EF$，$AF = DC$，$A$，$F$，$C$，$D$四点在同一直线上. 要利用“$SAS$”来判定$\triangle ABC\cong\triangle DEF$，下列四个条件中：①$∠A = ∠D$；②$∠ACB = ∠DFE$；③$AB// DE$；④$BC// EF$. 可以利用的是（ ）

A.①②
B.②④
C.②③
D.①④

答案： 2. B 【解析】
∵AF=DC，
∴AC=DF.
∵∠ACB=∠DFE，BC=EF，
∴△ABC≌△DEF(SAS)，
∴②正确.
∵BC//EF，
∴∠ACB=∠DFE，
∴△ABC≌△DEF(SAS)，
∴④正确.
∵添加∠A=∠D或AB//DE，均不能利用“SAS”判定△ABC≌△DEF，
∴①和③均错误.
∴可以利用的是②④.故选B.

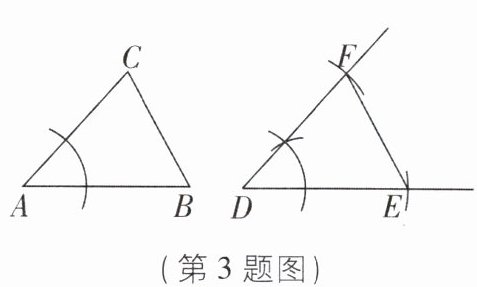
3 [2025 河南郑州期中]如图，已知$\triangle ABC$，用尺规作图的方法作出了$\triangle DEF\cong\triangle ABC$，请根据作图痕迹判断$\triangle DEF\cong\triangle ABC$的理论依据是______.

答案： 3. SAS 【解析】由作图可知，AC=DF，∠A=∠D，AB=DE，故△ABC≌△DEF(SAS).

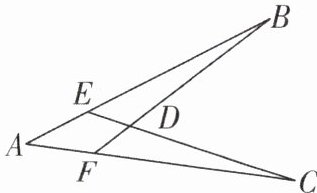
4 [2025 湖南长沙质检]如图，点$E$在$AB$上，点$F$在$AC$上，且$AE = AF$，$AB = AC$，$BF = 5$，$DE = 1$，则$DC$的长为（ ）

A.1
B.2
C.3
D.4

答案： 4. D 【解析】在△BAF和△CAE中，$\left\{\begin{array}{l} AF=AE,\\ ∠BAF=∠CAE,\\ AB=AC,\end{array}\right. $
∴△BAF≌△CAE(SAS)，
∴BF=CE.
∵BF=5，DE=1，
∴CD=CE - DE=BF - DE=5 - 1=4.故选D.

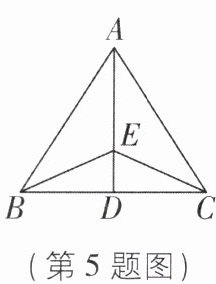
5 如图，已知$AB = AC$，$E$是角平分线$AD$上任意一点，则图中的全等三角形共有（ ）

A.0 对
B.1 对
C.2 对
D.3 对

答案： 5. D 【解析】
∵AD平分∠BAC，
∴∠BAD=∠CAD.
∵AB=AC，AD=AD，
∴△ADB≌△ADC(SAS)，
∴BD=CD，∠ADB=∠ADC.又
∵ED=ED，
∴△BDE≌△CDE.
∵AB=AC，∠BAE=∠CAE，AE=AE，
∴△ABE≌△ACE.综上，共有3对全等三角形.故选D.

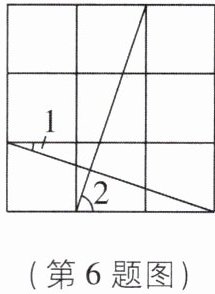
6 [2024 山东青岛期末]如图，在$3×3$的方格中，每个小方格的边长均为 1，则$∠1$与$∠2$的数量关系是______.

答案：
6. ∠1+∠2=90° 【解析】如图，在△ABC与△DEF中，$\left\{\begin{array}{l} BC=EF=1,\\ ∠ABC=∠DEF=90^{\circ },\\ AB=DE=3,\end{array}\right. $
∴△ABC≌△DEF(SAS)，
∴∠1=∠CAB.
∵∠CAB+∠2=90°，
∴∠1+∠2=90°.故答案为∠1+∠2=90°.

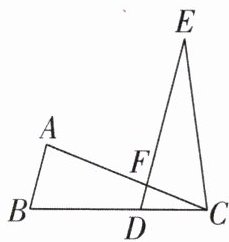
7 [2025 广东深圳期末]阅读并完成下列推理过程，在括号中填写依据. 如图，点$B$，$D$，$C$在同一直线上，$AB = CD$，$BC = DE$，$∠A = ∠CFD$，$CE = 8$，$CF = 3$，求$AF$的长.
证明：$\because ∠A = ∠CFD$（______），
$\therefore$______$//$______（ ），
$\therefore ∠B = ∠CDE$（ ）.
在$\triangle ABC$和$\triangle CDE$中，$AB = CD$（已知），
$∠B = ∠CDE$（ ），$BC = DE$（已知），
$\therefore \triangle ABC\cong\triangle CDE$（______），
$\therefore$______$= CE$（ ）.
$\because CE = 8$（已知），$\therefore AC =$______.
$\because CF = 3$（ ），$\therefore AF = AC - CF = 8 - 3 = 5$.

答案： 7. 已知 AB DE 同位角相等，两直线平行 两直线平行，同位角相等 已证 SAS AC 全等三角形对应边相等 8 已知(注:其中AB与DE可互换位置)
【解析】
∵∠A=∠CFD(已知)，
∴AB//DE(同位角相等，两直线平行)，
∴∠B=∠CDE(两直线平行，同位角相等).在△ABC和△CDE中，AB=CD(已知)，∠B=∠CDE(已证)，BC=DE(已知)，
∴△ABC≌△CDE(SAS)，
∴AC=CE(全等三角形对应边相等).
∵CE=8(已知)，
∴AC=8.
∵CF=3(已知)，
∴AF=AC - CF=8 - 3=5.故答案为已知；AB；DE；同位角相等，两直线平行；两直线平行，同位角相等；已证；SAS；AC；全等三角形对应边相等；8；已知.(注:其中AB与DE可互换位置)

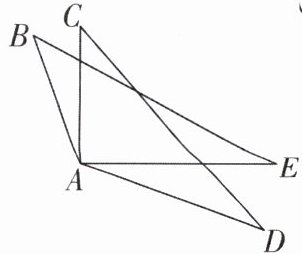
8 如图，$AB = AC$，$AE = AD$，要使$\triangle ACD\cong\triangle ABE$，需要补充的一个条件是（ ）

A.$∠B = ∠C$
B.$∠D = ∠E$
C.$∠BAC = ∠EAD$
D.$∠B = ∠E$

答案： 8. C 【解析】补充的条件是∠BAC=∠EAD，理由：因为∠BAC=∠EAD，所以∠BAC+∠CAE=∠EAD+∠CAE，所以∠BAE=∠CAD.在△ACD和△ABE中，$\left\{\begin{array}{l} AC=AB,\\ ∠CAD=∠BAE,\\ AD=AE,\end{array}\right. $所以△ACD≌△ABE(SAS).选项A、选项B、选项D的条件都不能推出△ACD≌△ABE，只有选项C的条件能推出△ACD≌△ABE.