《2025年初中必刷题八年级数学上册华师大版》

三、解答题(共58分)
15先化简,再求值：$(3x + 2y)^{2} - (3x + y)(3x - y)$,其中$x = \frac{1}{3}$,$y = -1$.

答案： 【解】原式$=(9x^{2}+12xy + 4y^{2})-(9x^{2}-y^{2})=9x^{2}+12xy + 4y^{2}-9x^{2}+y^{2}=12xy + 5y^{2}$.当$x=\frac {1}{3},y=-1$时，原式$=12× \frac {1}{3}× (-1)+5× (-1)^{2}=-4 + 5 = $.

16[2025湖南衡阳雁峰区校级调研](1)已知$a^{m} = 2$,$a^{n} = 3$,求$a^{2m + n}$的值；
(2)若$16^{m} = 4 × 2^{2n - 2}$,$27^{n} = 9 × 3^{m + 3}$,求$(m - n)^{2025}$的值.

答案： 【解】
(1)$\because a^{m}=2,a^{n}=3,\therefore$原式$=a^{2m}× a^{n}=(a^{m})^{2}× a^{n}=2^{2}× 3=4× 3=12$.
(2)$\because 16^{m}=4× 2^{2n - 2},\therefore 2^{4m}=2^{2}× 2^{2n - 2}=2^{2n},\therefore n = 2m.\because 27^{n}=9× 3^{m + 3},\therefore 3^{3n}=3^{m + 5},\therefore 3n = m + 5,\therefore 6m = m + 5,\therefore m = 1,\therefore n = 2,\therefore$原式$=(1 - 2)^{2025}=-1$.

17[2025河北石家庄期末]【提出问题】在数学课上,老师提出一个问题：“任意奇数的平方减去$1后都一定是8$的倍数吗？”
(1)【解决问题】计算：$3^{2} - 1 = $______；$5^{2} - 1 = $______；$7^{2} - 1 = $______.以上计算结果均______(填“是”或“不是”)$8$的倍数.
(2)设一个奇数为$2n + 1$($n$为整数),请你先试着回答老师提出的问题,再验证你的结论.
(3)【拓展延伸】任意奇数的平方加上$1$后都一定是______的倍数.

答案： 【解】
(1)$3^{2}-1=8;5^{2}-1=24;7^{2}-1=48$，以上计算结果均是8的倍数.故答案为8,24,48,是.
(2)一定是8的倍数.验证：这个奇数为$2n + 1$，则有$(2n + 1)^{2}-1=2n(2n + 2)=4n(n + 1)$.又因为n,$n + 1$为两个连续整数，故其中必有一个是2的倍数，所以$(2n + 1)^{2}-1$一定是8的倍数.
(3)2.

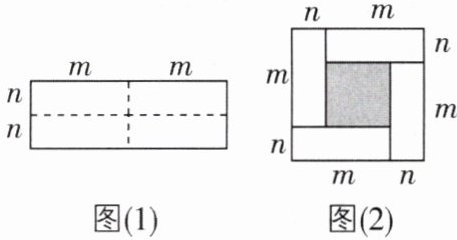
18[2025吉林长春德惠期中]图(1)是一个长为$2m$,宽为$2n$的长方形,沿图中虚线用剪刀将其剪成四个相同的小长方形,然后按图(2)所示方式拼成一个正方形.
(1)请用两种不同的方法表示图(2)中阴影部分的面积.
方法一：______；方法二：______.
(2)观察图(2),写出代数式$(m + n)^{2}$,$(m - n)^{2}$,$mn$之间的等量关系：______.
(3)利用(2)得到的等量关系,解决如下问题：
若$a - b = 4$,$ab = 5$,求$a + b$的值.

答案： 【解】
(1)方法一：$(m - n)^{2}$；方法二：$(m + n)^{2}-4mn$.故答案为$(m - n)^{2},(m + n)^{2}-4mn$.
(2)$(m + n)^{2}=(m - n)^{2}+4mn$，故答案为$(m + n)^{2}=(m - n)^{2}+4mn$.
(3)由
(2)可知，$(a + b)^{2}=(a - b)^{2}+4ab$.$\because a - b = 4,ab = 5,\therefore (a + b)^{2}=4^{2}+4× 5=36,\therefore a + b=\pm 6$.

19[2025陕西榆林期末]分解因式$x^{4} + 4$时该式只有两项,且属于平方和,要使用公式可以添一项$4x^{2}$,随即将此项$4x^{2}$减去,即可得$x^{4} + 4 = x^{4} + 4x^{2} + 4 - 4x^{2} = (x^{2} + 2)^{2} - 4x^{2} = (x^{2} + 2)^{2} - (2x)^{2} = (x^{2} + 2x + 2)(x^{2} - 2x + 2)$.
根据以上方法,把下列各式因式分解：
(1)$4x^{4} + y^{4}$；
(2)$a^{2} - 4am - n^{2} + 4mn$.

答案： 【解】
(1)原式$=4x^{4}+y^{4}+4x^{2}y^{2}-4x^{2}y^{2}=(2x^{2}+y^{2})^{2}-4x^{2}y^{2}=(2x^{2}+y^{2}+2xy)(2x^{2}+y^{2}-2xy)$.
(2)原式$=a^{2}-4am + 4m^{2}-4m^{2}-n^{2}+4mn=(a^{2}-4am + 4m^{2})-(4m^{2}+n^{2}-4mn)=(a - 2m)^{2}-(2m - n)^{2}=(a - 2m + 2m - n)(a - 2m - 2m + n)=(a - n)(a - 4m + n)$.