《2025年初中必刷题八年级数学上册华师大版》

1[2025江苏南通期中,中]如图,在△ABC中,∠ACB= 118°,将△ABC绕点A顺时针旋转得到△ADE,点C的对应点E恰好落在BC边的延长线上,则∠CAE的度数是( )

A.56°
B.58°
C.60°
D.62°

答案： A 【解析】
∵将△ABC 绕点 A 顺时针旋转得到△ADE，
∴△ABC≌△ADE，
∴AC=AE.
∵B，C，E 三点在同一直线上，∠ACB=118°，
∴∠AEC=∠ACE=62°，
∴∠CAE=180°-∠AEC-∠ACE=56°，故选 A.

2[2024广西玉林期中,中]如图,△ABC中,AB= AC= 13,S△ABC= 65,AD是∠BAC的平分线,E是AD边上的动点,F是AB边上的动点,则BE+EF的最小值为______.

答案： 10 【解析】过点 C 作 CG⊥AB 于点 G，连结 CE，如图.
∵AB=AC=13，AD 是∠BAC 的平分线，
∴AD⊥BC，BD=DC，
∴点 B，C 关于 AD 对称，
∴BE=CE，
∴BE+EF=CE+EF.根据连结直线外一点与直线上各点的所有线段中，垂线段最短，可得 BE+EF=CE+EF≥CG，即 BE+EF 的最小值为 CG 的长.
∵△ABC 的面积为 65，
∴$S_{\triangle ABC}=\frac{1}{2}AB\cdot CG=\frac{1}{2}×13× CG=65$，
∴CG=10，即 BE+EF 的最小值为 10.故答案为 10.

3[中]如图,已知$∠BAC= 80°,A_1,B_1$分别是射线AC,线段$A_1B$上的点,且$A_1B= AB.A_2,B_2$分别是射线$A_1C,$线段$A_2B_1$上的点,且$A_1A_2= A_1B_1;A_3,B_3$分别是射线$A_2C,$线段$A_3B_2$上的点,且$A_2A_3= A_2B_2;…;$以此类推,则$∠A_3A_4B_3$的度数为______°.

答案： 10 【解析】
∵∠BAC=80°，$A_1B=AB$，
∴∠BAC=∠$BA_1A$=80°.
∵$A_1A_2=A_1B_1$，
∴∠$A_1A_2B_1$=∠$A_1B_1A_2$=$\frac{1}{2}\angle BA_1A=\frac{1}{2}×80^{\circ}=40^{\circ}$.
∵$A_2A_3=A_2B_2$，
∴∠$A_2A_3B_2$=∠$A_2B_2A_3$=$\frac{1}{2}\angle A_1A_2B_1=\frac{1}{2}×40^{\circ}=20^{\circ}$.
∵$A_3A_4=A_3B_3$，
∴∠$A_3A_4B_3$=∠$A_3B_3A_4$=$\frac{1}{2}\angle A_2A_3B_2=\frac{1}{2}×20^{\circ}=10^{\circ}$.故答案为 10.

4[较难]如图,在△ABC中,AB= AC= 24厘米,BC= 16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

答案： 4 或6【解析】设经过 x 秒后能使△BPD 与△CQP 全等.
∵AB=AC=24 厘米，点 D 为 AB 的中点，
∴BD=12 厘米，∠ABC=∠ACB，
∴要使△BPD 与△CQP 全等，则 BD=CP 或 BP=CP，即 12=16-4x 或 4x=16-4x，解得 x=1 或 x=2.当 x=1 时，BP=CQ=4，4÷1=4（厘米/秒）；当 x=2 时，BD=CQ=12，12÷2=6（厘米/秒）.即点 Q 的运动速度是 4 厘米/秒或 6 厘米/秒.

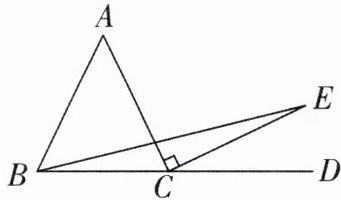
5[2025广东珠海斗门区期末,中]如图,在等腰三角形ABC中,AB= AC,D为BC延长线上一点,EC⊥AC且EC= AC,垂足为C,连结BE,若BC= 6,求△BCE的面积.

答案： 【解】过 A 作 AH⊥BC 于 H，过 E 作 EF⊥BC 于 F，如图.
∵AB=AC，BC=6，
∴BH=HC=3.
∵∠ACE=90°，
∴∠ACH+∠ECF=90°.
∵∠AHC=90°，
∴∠CAH+∠ACH=90°，
∴∠ECF=∠CAH.在△ACH 与△CEF 中，$\begin{cases}\angle AHC=\angle CFE,\\\angle CAH=\angle ECF,\\AC=CE,\end{cases}$
∴△ACH≌△CEF(AAS)，
∴EF=CH=3，
∴△BCE 的面积为$\frac{1}{2}BC\cdot EF=\frac{1}{2}×6×3=9$.

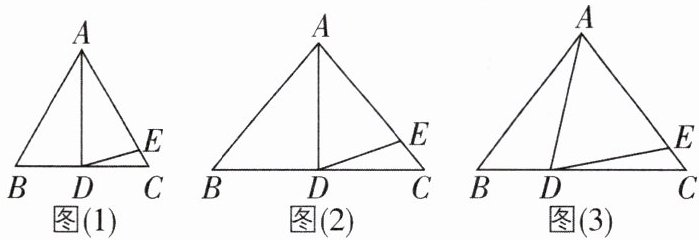
6核心素养推理能力[难]在△ABC中,AB= AC.
(1)如图(1),如果∠BAD= 30°,AD是BC边上的高,AD= AE,则∠EDC= ______.
(2)如图(2),如果∠BAD= 40°,AD是BC边上的高,AD= AE,则∠EDC= ______.
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示.
(4)如图(3),如果AD不是BC边上的高,AD= AE,上述关系是否仍成立?如果成立,请说明理由.

答案： （1）15° 【解析】
∵在△ABC 中，AB=AC，AD 是 BC 边上的高，
∴∠CAD=∠BAD=30°，∠ADC=90°.
∵AD=AE，
∴∠ADE=∠AED=75°，
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.故答案为 15°.
（2）20° 【解析】
∵在△ABC 中，AB=AC，AD 是 BC 边上的高，
∴∠CAD=∠BAD=40°，∠ADC=90°.
∵AD=AE，
∴∠ADE=∠AED=70°，
∴∠EDC=∠ADC-∠ADE=90°-70°=20°.故答案为 20°.
（3）∠BAD=2∠EDC（或∠EDC=$\frac{1}{2}\angle BAD$）.
（4）仍成立，理由如下：
∵AD=AE，
∴∠ADE=∠AED，
∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=（∠EDC+∠C）+∠EDC=2∠EDC+∠C.又
∵AB=AC，
∴∠B=∠C，
∴∠BAD=2∠EDC.