《2025年初中必刷题八年级数学上册华师大版》

1 [2024重庆渝中区期末]如图,在$\triangle ABC$中,$AB = AC$,$\angle A = 42^{\circ}$,$AB的垂直平分线MN交AC于D$点,连结$BD$,则$\angle DBC$的度数是( )

A.$22^{\circ}$
B.$27^{\circ}$
C.$32^{\circ}$
D.$40^{\circ}$

答案： B　[解析]
∵在△ABC中,AB=AC,∠A=42°,根据等腰三角形的性质,求得∠ABC=∠ACB=69°.
∵AB的垂直平分线MN交AC于点D,
∴AD=BD,
∴∠ABD=∠A=42°,
∴∠DBC=∠ABC−∠ABD=27°,故选B.

2 如图,在$\triangle ABC$中,$\angle A = 45^{\circ}$,$\angle B = 30^{\circ}$。用直尺和圆规在边$AB上确定一点D$,连结$CD$,则$\angle ACD$的大小为( )

A.$60^{\circ}$
B.$75^{\circ}$
C.$65^{\circ}$
D.$70^{\circ}$

答案： B　[解析]由尺规作图可知，线段BC的垂直平分线交AB于D,
∴DC=DB,
∴∠DCB=∠B=30°.
∵∠A=45°,∠B=30°,
∴∠ACB=180°−∠A−∠B=105°,
∴∠ACD=∠ACB−∠DCB=75°,故选B.

3 [2024山西吕梁期末]如图,$\triangle ABC$中,$AB = AE$,且$AD \perp BC于点D$,$EF垂直平分AC$,交$AC于点F$,交$BC于点E$,若$\triangle ABC的周长为16$,$AC = 6$,则$DC$的长为( )

A.$5$
B.$8$
C.$9$
D.$10$

答案： A　[解析]
∵△ABC的周长为16,
∴AB+BC+AC=16.又
∵AC=6,
∴AB+BC=10.
∵EF垂直平分AC,
∴EA=EC;
∵AB=AE,AD⊥BC,
∴BD=DE,
∴AB+BD=AE+DE=CE+ED=$\frac{1}{2}$×(AB+BC)=5,
∴DC=DE+EC=5,故选A.

4 [2025河北承德质检]如图,直线$l是线段AB$的垂直平分线,点$C在直线l$外,且与$A点在直线l$的同一侧,连结$BC$,交直线$l于点D$,点$P是直线l$上的一点(不与点$D$重合),连结$AP$,$CP$。记$m = BC$,$n = AP + PC$,则正确的是( )

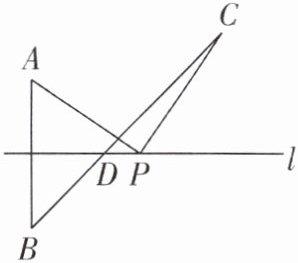
A.$m ＞ n$
B.$m = n$
C.$m ＜ n$
D.无法比较$m与n$的大小

答案：
C　[解析]如图,连结BP.
∵直线l是线段AB的垂直平分线，
∴AP=BP,
∴AP+CP=BP+CP.
∵BP+CP＞BC,m=BC,n=AP+PC,
∴m＜n,故选C.

5 宇树科技正在测试一款新型巡逻机器人。如图,该机器人(点$P$)按照预设的路径(直线$MN$)巡逻。路径附近有一个等边三角形的信号发射区$ABC$,当机器人(点$P$)与信号发射区的任意两个顶点距离相等时,就会触发警报。若直线$MN//BC$,则在直线$MN$上会触发警报的点有( )

A.$1$个
B.$2$个
C.$3$个
D.$4$个

答案： C　[解析]根据垂直平分线的性质易知，直线MN上会触发警报的点有AB,AC,BC的垂直平分线分别与直线MN的交点，共3个.故选C.

6 如图,$\triangle ABC$中,$AB的垂直平分线分别交AB$,$BC于点D$,$E$,$AC的垂直平分线分别交AC$,$BC于点F$,$G$,连结$AE$,$AG$。
(1)若$\triangle AEG的周长为10$,求线段$BC$的长；
(2)若$\angle BAC = 104^{\circ}$,求$\angle EAG$的度数。

答案：
(1)
∵DE垂直平分AB,GF垂直平分AC,
∴EA=EB,GA=GC.
∵△AEG的周长为10,即AE+EG+AG=10,
∴BC=BE+EG+GC=AE+EG+GA=10.
(2)
∵∠BAC=104°,
∴∠B+∠C=180°−104°=76°.
∵EA=EB,GA=GC,
∴∠EAB=∠B,∠GAC=∠C,
∴∠EAB+∠GAC=∠B+∠C=76°,
∴∠EAG=∠BAC−(∠EAB+∠GAC)=104°−76°=28°.

7 [2025四川遂宁期中]将$\triangle ABC$按如图所示方式折叠,使点$C的对应点C'与点B$重合,折痕为$DE$,则$DE$( )

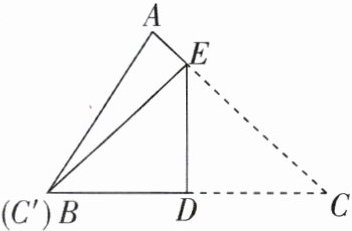
A.是$\triangle ABC$的一条角平分线
B.是$\triangle ABC$的一条高线
C.是$\triangle ABC$的一条中线
D.垂直平分边$BC$

答案： D　[解析]由折叠可得BD=CD,BE=CE,
∴DE垂直平分边BC,故选D.

8 [2025浙江金华质检]如图,已知$AB平分\angle CAD$,$AC = AD$,$E在线段AB$上,有以下结论：①$BC = BD$；②$CE = DE$；③$BA平分\angle CBD$；④$AB所在的直线是CD$的垂直平分线,其中正确的是____。(填序号)

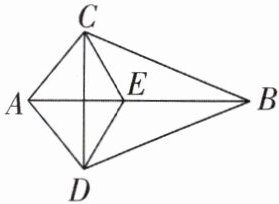
答案： ①②③④　[解析]
∵AB平分∠CAD,
∴∠CAB=∠DAB.又
∵AC=AD,AB=AB,
∴△ABC≌△ABD(SAS),
∴BC=BD,∠ABC=∠ABD,即BA平分∠CBD,故①③正确.又
∵AC=AD,
∴AB所在的直线是CD的垂直平分线，故④正确.
∵E在直线AB上,
∴CE=DE,故②正确，故答案为①②③④.