《2025年初中必刷题八年级数学上册华师大版》

1 [2025陕西延安期末]计算$(14a^{3}b^{2}-7ab^{2})÷7ab^{2}$的结果是 ( )

A.$2a^{2}$
B.$2a^{2}-1$
C.$2a^{2}-b$
D.$2a^{2}b-1$

答案： B【解析】$(14a^{3}b^{2}-7ab^{2})÷7ab^{2}=14a^{3}b^{2}÷7ab^{2}-7ab^{2}÷7ab^{2}=2a^{2}-1$.故选B.

2 下列各式,计算结果错误的是 ( )

A.$(3a^{2}+2a-6ab)÷2a= \frac {3}{2}a-3b+1$
B.$(-4a^{3}+12a^{2}b-7a^{3}b^{2})÷(-4a^{2})= a-3b+\frac {7}{4}ab^{2}$
C.$(4x^{m+2}-5x^{m-1})÷3x^{m-2}= \frac {4}{3}x^{4}-\frac {5}{3}$
D.$(3a^{n+1}+a^{n+2}-12a^{n})÷(-24a^{n})= -\frac {1}{8}a-\frac {1}{24}a^{2}+\frac {1}{2}$

答案： C【解析】A选项，$(3a^{2}+2a-6ab)÷2a=\frac {3}{2}a-3b+1$,故此选项正确；B选项，$(-4a^{3}+12a^{2}b-7a^{3}b^{2})÷(-4a^{2})=a-3b+\frac {7}{4}ab^{2}$,故此选项正确；C选项，$(4x^{m+2}-5x^{m-1})÷3x^{m-2}=\frac {4}{3}x^{4}-\frac {5}{3}x$,故此选项不正确；D选项，$(3a^{n+1}+a^{n+2}-12a^{n})÷(-24a^{n})=-\frac {1}{8}a-\frac {1}{24}a^{2}+\frac {1}{2}$,故此选项正确.

3 [2025福建泉州晋江期中]计算:
(1)$(8m^{3}n^{2}-4m^{2}-2m)÷(-2m);$
(2)$(2x^{2}y^{4}-8xy^{3}+x^{3}y^{2})÷(-4xy^{2});$
(3)$(16m^{6}n^{4}-8m^{4}n^{2}+4m^{2}n^{2})÷(-2mn)^{2};$
(4)$[x(x^{2}y^{2}-xy)-y(x^{2}-x^{3}y)]÷3x^{2}y.$

答案： 【解】
(1)原式$=8m^{3}n^{2}÷(-2m)-4m^{2}÷(-2m)-2m÷(-2m)=-4m^{2}n^{2}-(-2m)-(-1)=-4m^{2}n^{2}+2m+1.$
(2)原式$=2x^{2}y^{4}÷(-4xy^{2})+8xy^{3}÷4xy^{2}-x^{3}y^{2}÷4xy^{2}=-\frac {1}{2}xy^{2}+2y-\frac {1}{4}x^{2}.$
(3)原式$=(16m^{6}n^{4}-8m^{4}n^{2}+4m^{2}n^{2})÷4m^{2}n^{2}=16m^{6}n^{4}÷4m^{2}n^{2}-8m^{4}n^{2}÷4m^{2}n^{2}+4m^{2}n^{2}÷4m^{2}n^{2}=4m^{4}n^{2}-2m^{2}+1.$
(4)原式$=(x^{3}y^{2}-x^{2}y-x^{2}y+x^{3}y^{2})÷3x^{2}y=(2x^{3}y^{2}-2x^{2}y)÷3x^{2}y=\frac {2}{3}xy-\frac {2}{3}.$

4 某市“旧城改造”中,计划在市内一块长方形空地上种植草皮,以美化环境.已知长方形空地的面积为$(3ab+b)$平方米,宽为$b$米,则这块空地的长为 ( )

A.$3a$米
B.$(3a+1)$米
C.$(3a+2b)$米
D.$(3ab^{2}+b^{2})$米

答案： B【解析】
∵长方形空地的面积为$(3ab+b)$平方米，宽为b米，
∴这块空地的长为$(3ab+b)÷b=(3a+1)$米.故选B.

5 [2025湖南衡阳质检]计算$3x$加上一个多项式时,错将加法写成了乘法,得到的结果是$6x^{3}-3x^{2}+3x$,由此可以推断出正确的计算结果是 ( )

A.$x^{2}+2x-1$
B.$2x^{2}+2x+1$
C.$2x^{2}-2x-1$
D.$x^{2}-4x+1$

答案： B【解析】由题意可知，这个多项式为$(6x^{3}-3x^{2}+3x)÷3x=2x^{2}-x+1$，
∴正确的计算结果是$2x^{2}-x+1+3x=2x^{2}+2x+1$,故选B.

6 [2025上海普陀区期中]已知$(x^{n+a}+x^{n+b})÷x^{n+1}= x^{2}+x^{3}$,其中$n$是正整数,那么$a+b$的值是 ( )

A.3
B.5
C.7
D.9

答案： C【解析】$\because (x^{n+a}+x^{n+b})÷x^{n+1}=x^{2}+x^{3},\therefore x^{n+a}÷x^{n+1}+x^{n+b}÷x^{n+1}=x^{2}+x^{3},\therefore x^{a-1}+x^{b-1}=x^{2}+x^{3},\therefore a-1=2,b-1=3$或$a-1=3,b-1=2,\therefore a=3,b=4$或$a=4,b=3,\therefore a+b=3+4=7$或$a+b=4+3=7$.故选C.

7 已知多项式$2x^{3}-4x^{2}-1除以一个多项式A$,商式为$2x$,余式为$x-1$,则这个多项式$A= $ ____.

答案： $x^{2}-2x-\frac {1}{2}$【解析】$A=[(2x^{3}-4x^{2}-1)-(x-1)]÷2x=(2x^{3}-4x^{2}-x)÷2x=x^{2}-2x-\frac {1}{2}.$

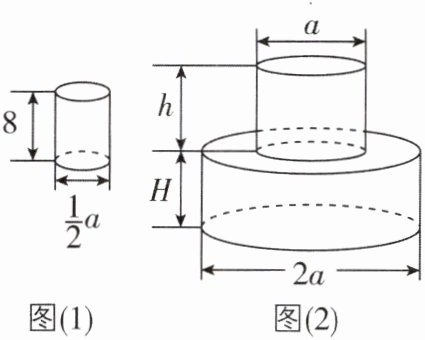
8 [2025四川成都期末]将如图(1)所示的杯子中盛满水,如果将这个杯子中的水全部倒入如图(2)所示的瓶子(两个圆柱)中,那么一共需要 ____杯水才能将这个瓶子装满.

答案： $(2H+\frac {1}{2}h)$【解析】题图
(2)中瓶子的上半部分的体积为$π(\frac {a}{2})^{2}h$,题图
(2)中瓶子的下半部分的体积为$πa^{2}H$,
∴题图
(2)中瓶子的体积为$π(\frac {a}{2})^{2}h+πa^{2}H=\frac {1}{4}πa^{2}h+πa^{2}H=(\frac {1}{4}h+H)πa^{2}$.题图
(1)中杯子的体积为$π(\frac {1}{4}a)^{2}×8=\frac {1}{2}πa^{2}$,
∴一共需要$(\frac {1}{4}h+H)πa^{2}÷\frac {1}{2}πa^{2}=(2H+\frac {1}{2}h)$杯水才能将这个瓶子装满,故答案为$(2H+\frac {1}{2}h).$

9 [2024山西吕梁期中]先化简,再求值:$(x-2y)^{2}+(2x+y)^{2}+(8x^{2}y^{2}-20xy^{3})÷4xy$,其中$x= \frac {1}{5},y= 5.$

答案： 【解】原式$=x^{2}-4xy+4y^{2}+4x^{2}+4xy+y^{2}+2xy-5y^{2}=5x^{2}+2xy$.当$x=\frac {1}{5},y=5$时,原式$=5×(\frac {1}{5})^{2}+2×\frac {1}{5}×5=\frac {11}{5}.$