《2025年初中必刷题八年级数学上册华师大版》

1 下列多项式乘法中,能用平方差公式计算的是( )

A.$(\frac{1}{2}m - n)(m + \frac{1}{2}n)$
B.$(-m - n)(m + n)$
C.$(-m - n)(m - n)$
D.$(m - n)(n - m)$

答案： C 【解析】
∵$\left( \frac{1}{2}m-n \right)\left( m+\frac{1}{2}n \right)$不符合平方差公式的特点，
∴选项 A 不符合题意；
∵$(-m-n)(m+n)=-(m+n)^2$，
∴选项 B 不符合题意；
∵$(-m-n)(m-n)=-(m+n)(m-n)=-(m^2-n^2)$，
∴选项 C 符合题意；
∵$(m-n)(n-m)=-(m-n)^2$，
∴选项 D 不符合题意.故选 C.

2 [2024 山东滨州期末]在运用乘法公式计算$(x + 2y - 1)(x - 2y + 1)$时,下列变形正确的是( )

A.$[x - (2y + 1)]^2$
B.$x^2 - (2y - 1)^2$
C.$(x - 2y)^2 - 1$
D.$[x + (2y + 1)]^2$

答案： B 【解析】$(x+2y-1)(x-2y+1)=[x+(2y-1)][x-(2y-1)]=x^2-(2y-1)^2$. 故选 B.

3 若$a^4 = 3$,则$(1 - a)\cdot(1 + a)(1 + a^2)$的值为____.

答案： -2 【解析】原式$=(1-a^2)(1+a^2)=1-a^4=1-3=-2$，故答案为-2.

4 计算:(1)$b(a + b) + (a + b)(a - b)$.
(2)$(3x + 2y)(3x - 2y) - 3x(x + 2y)$.

答案： 【解】
(1)$b(a+b)+(a+b)(a-b)=ab+b^2+a^2-b^2=ab+a^2$.
(2)$(3x+2y)(3x-2y)-3x(x+2y)=9x^2-4y^2-3x^2-6xy=6x^2-6xy-4y^2$.

5 [2025 四川宜宾期末]若$a^2 - b^2 = 4$,则$(a + b)^2\cdot(a - b)^2$的值是( )

A.24
B.16
C.8
D.4

答案： B 【解析】
∵$(a+b)^2(a-b)^2=[(a+b)(a-b)]^2=(a^2-b^2)^2$，$a^2-b^2=4$，
∴$(a+b)^2(a-b)^2=(a^2-b^2)^2=4^2=16$. 故选 B.

6 如图,阴影部分是边长为$a的大正方形中剪去一个边长为b$的小正方形后所得到的图形,将阴影部分通过割、拼的方式形成新的图形,给出四种割拼方法,其中能够验证平方差公式的有( )


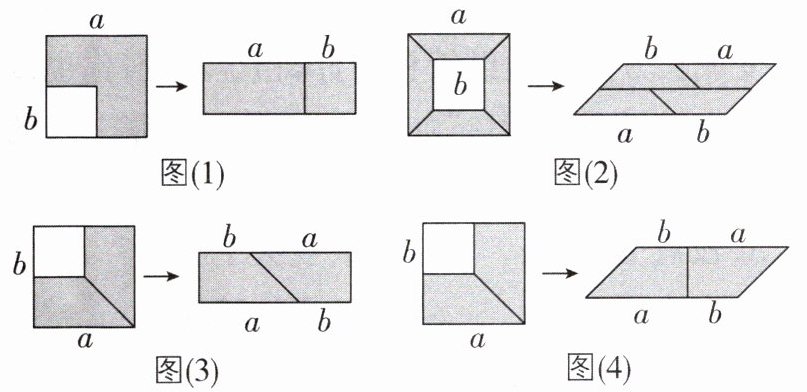
A.1种
B.2种
C.3种
D.4种

答案： D 【解析】题图
(1)拼接前的面积为$a^2-b^2$，拼接后的面积为$(a+b)(a-b)=a^2-b^2$，能验证平方差公式；题图
(2)拼接前的面积为$a^2-b^2$，拼接后的面积为$(a+b)(a-b)=a^2-b^2$，能验证平方差公式；题图
(3)拼接前的面积为$a^2-b^2$，拼接后的面积为$(a+b)(a-b)=a^2-b^2$，能验证平方差公式；题图
(4)拼接前的面积为$a^2-b^2$，拼接后的面积为$(a+b)(a-b)=a^2-b^2$，能验证平方差公式. 综上，四种方法都能验证平方差公式. 故选 D.

7 [2025 山东菏泽期末]若三角形的一边长为$2a + 3$,该边上的高为$2a - 3$,则此三角形的面积是____.

答案： $2a^2-\frac{9}{2}$ 【解析】此三角形的面积为$\frac{1}{2}(2a+3)(2a-3)=\frac{1}{2}(4a^2-9)=2a^2-\frac{9}{2}$，故答案为$2a^2-\frac{9}{2}$.

8 [2025 山东德州陵城区期末]若$(a^2 + b^2 + 1)(a^2 + b^2 - 1) = 35$,则$a^2 + b^2 = $____.

答案： 6 【解析】
∵$(a^2+b^2+1)(a^2+b^2-1)=35$，
∴$[(a^2+b^2)+1][(a^2+b^2)-1]=35$，
∴$(a^2+b^2)^2-1=35$，
∴$(a^2+b^2)^2=36$.
∵$a^2+b^2\geq0$，
∴$a^2+b^2=6$.

9 [2024 山西临汾期末]已知$a^2 - b^2 = - 1$,则$(a + b)^{2023}(b - a)^{2023} = $____.

答案： 1 【解析】
∵$a^2-b^2=-1$，
∴$b^2-a^2=1$，
∴$(a+b)^{2023}(b-a)^{2023}=[(a+b)(b-a)]^{2023}=(b^2-a^2)^{2023}=1^{2023}=1$，故答案为 1.

10 [2024 北京东城区期末]若$(x + y^2)(x - y^2)\cdot(x^2 + y^4) = x^m - y^n$,则$\sqrt{m} - \sqrt[3]{n} = $____.

答案： 0 【解析】$(x+y^2)(x-y^2)(x^2+y^4)=(x^2-y^4)(x^2+y^4)=x^4-y^8=x^m-y^n$，
∴$m=4$，$n=8$，
∴$\sqrt{m}-\sqrt[3]{n}=\sqrt{4}-\sqrt[3]{8}=2-2=0$. 故答案为 0.

11 利用乘法公式有时能进行简便计算.
例:$102×98 = (100 + 2)(100 - 2) = 100^2 - 2^2 = 10000 - 4 = 9996$.
请参考给出的例题,利用简便方法计算:(1)$31×29$;(2)$195×205$.

答案： 【解】
(1)$31×29=(30+1)×(30-1)=30^2-1^2=900-1=899$.
(2)$195×205=(200-5)×(200+5)=200^2-5^2=40000-25=39975$.