第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2025海南儋州期中,中]下列命题:
①若$2m = 2,2n = 4$,则$2m + n = 6;$
②若$x^{2}-6x + k^{2}$恰好是另一个整式的平方,则常数k的值为3;
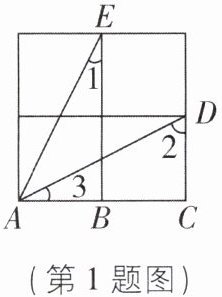
③若下图是由4个全等的小正方形拼成,则$∠1 + ∠2 = 90^{\circ };$
④有一个角及两条边分别对应相等的两个三角形全等. 其中假命题有 ( )
①若$2m = 2,2n = 4$,则$2m + n = 6;$
②若$x^{2}-6x + k^{2}$恰好是另一个整式的平方,则常数k的值为3;
③若下图是由4个全等的小正方形拼成,则$∠1 + ∠2 = 90^{\circ };$
④有一个角及两条边分别对应相等的两个三角形全等. 其中假命题有 ( )

答案:
C [解析]①若2m=2,2n=4,则n=2,
∴2m+n=2+2=4,故①为假命题;②若x² - 6x + k²恰好是另一个整式的平方,则常数k的值为±3,故②为假命题;③由题图可知,AB=CD,∠ABE=∠DCA=90°,BE=AC,
∴△ABE≌△DCA(SAS),
∴∠1=∠3,
∴∠1+∠2=∠3+∠2=90°,故③为真命题;④有一个角及两条边分别对应相等的两个三角形不一定全等,当角为两边的夹角时全等,故④为假命题.综上,假命题有3个,故选C.
∴2m+n=2+2=4,故①为假命题;②若x² - 6x + k²恰好是另一个整式的平方,则常数k的值为±3,故②为假命题;③由题图可知,AB=CD,∠ABE=∠DCA=90°,BE=AC,
∴△ABE≌△DCA(SAS),
∴∠1=∠3,
∴∠1+∠2=∠3+∠2=90°,故③为真命题;④有一个角及两条边分别对应相等的两个三角形不一定全等,当角为两边的夹角时全等,故④为假命题.综上,假命题有3个,故选C.
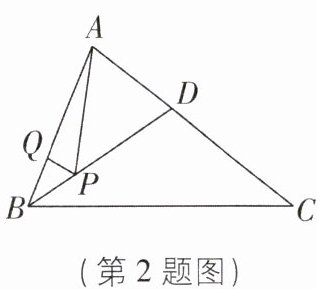
2 [2025四川宜宾期末,中]如图,在$△ABC$中,$∠ABC = 68^{\circ },BD$平分$∠ABC$,P为线段BD上一动点,Q为边AB上一动点,当$AP + PQ$的值最小时,$∠APQ$的度数为 ( )
A.$22^{\circ }$
B.$34^{\circ }$
C.$56^{\circ }$
D.$68^{\circ }$

A.$22^{\circ }$
B.$34^{\circ }$
C.$56^{\circ }$
D.$68^{\circ }$
答案:
D [解析]在BC上截取BE=BQ,连结PE,如图所示.
∵BD平分∠ABC,
∴∠ABD=∠CBD=$\frac{1}{2}$∠ABC = 34°.在△BQP和△BEP中,{BQ=BE,∠ABD=∠CBD,BP=BP,
∴△BQP≌△BEP(SAS),
∴PQ=PE,∠BPQ=∠BPE,
∴AP+PQ=AP+PE.
∵垂线段最短,
∴当点A,P,E在同一直线上,且AE⊥BC时,AP+PE的值最小,即AP+PQ的值最小,此时∠AEB=90°.
∵∠CBD=34°,
∴∠BPE=90° - 34°=56°,
∴∠BPQ=∠BPE=56°,
∴∠APQ=180° - ∠BPQ - ∠BPE=180° - 56° - 56°=68°,故选D.
D [解析]在BC上截取BE=BQ,连结PE,如图所示.

∵BD平分∠ABC,
∴∠ABD=∠CBD=$\frac{1}{2}$∠ABC = 34°.在△BQP和△BEP中,{BQ=BE,∠ABD=∠CBD,BP=BP,
∴△BQP≌△BEP(SAS),
∴PQ=PE,∠BPQ=∠BPE,
∴AP+PQ=AP+PE.
∵垂线段最短,
∴当点A,P,E在同一直线上,且AE⊥BC时,AP+PE的值最小,即AP+PQ的值最小,此时∠AEB=90°.
∵∠CBD=34°,
∴∠BPE=90° - 34°=56°,
∴∠BPQ=∠BPE=56°,
∴∠APQ=180° - ∠BPQ - ∠BPE=180° - 56° - 56°=68°,故选D.
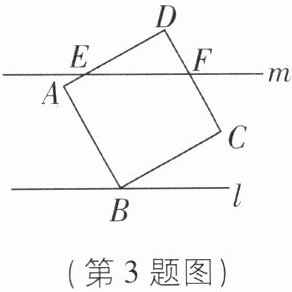
3 [2025河南濮阳期中,中]如图,正方形ABCD的顶点B在直线l上,将直线l向上平移线段AB的长得到直线m,直线m分别交AD,CD于点E,F. 若求$△DEF$的周长,则只需知道( )
A.AB的长
B.FE的长
C.DE的长
D.DF的长

A.AB的长
B.FE的长
C.DE的长
D.DF的长
答案:
A [解析]如图,过B作BH⊥m于H,连结BE,BF.
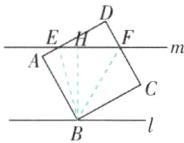
∵直线l向上平移线段AB的长度得到直线m,
∴BH=AB.又
∵∠A=∠BHE=90°,EB=EB,
∴Rt△AEB≌Rt△HEB,
∴AE=EH.同理得Rt△FCB≌Rt△FHB,
∴HF=CF,
∴△DEF的周长为DE+EF+DF=DE+EH+HF+DF=DE+AE+CF+DF=AD+CD=2AB.
∴求△DEF的周长,只需知道AB的长.故选A.
A [解析]如图,过B作BH⊥m于H,连结BE,BF.

∵直线l向上平移线段AB的长度得到直线m,
∴BH=AB.又
∵∠A=∠BHE=90°,EB=EB,
∴Rt△AEB≌Rt△HEB,
∴AE=EH.同理得Rt△FCB≌Rt△FHB,
∴HF=CF,
∴△DEF的周长为DE+EF+DF=DE+EH+HF+DF=DE+AE+CF+DF=AD+CD=2AB.
∴求△DEF的周长,只需知道AB的长.故选A.
4 [中]如图,在$△ACD$中,$∠CAD = 90^{\circ },AC = 4,AD = 6,AB// CD$,E是CD上一点,BE交AD于点F,若$AB = DE$,则图中阴影部分的面积为 _ .
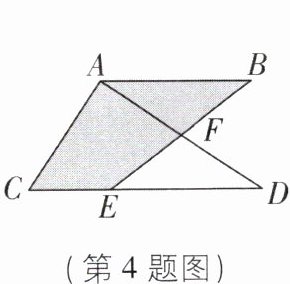

答案:
12 [解析]
∵AB//CD,
∴∠B=∠FED,∠FAB=∠D.在△ABF和△DEF中,{∠B=∠FED,AB=DE,∠FAB=∠D,
∴△ABF≌△DEF(ASA),
∴S△ABF=S△DEF.
∵∠CAD=90°,AC=4,AD=6,
∴S阴影部分=S四边形ACEF+S△ABF=S四边形ACEF+S△DEF=S△ACD=$\frac{1}{2}$×4×6=12.故答案为12.
∵AB//CD,
∴∠B=∠FED,∠FAB=∠D.在△ABF和△DEF中,{∠B=∠FED,AB=DE,∠FAB=∠D,
∴△ABF≌△DEF(ASA),
∴S△ABF=S△DEF.
∵∠CAD=90°,AC=4,AD=6,
∴S阴影部分=S四边形ACEF+S△ABF=S四边形ACEF+S△DEF=S△ACD=$\frac{1}{2}$×4×6=12.故答案为12.
5 [中]如图,在四边形ABCD中,$AB = CD,∠DAC + ∠BCA = 180^{\circ },∠B + ∠D = 90^{\circ }$,且四边形ABCD的面积是18,则CD的长为 _ .
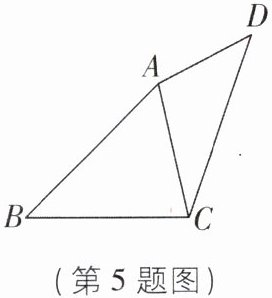

答案:
6 [解析]如图,延长BC到E,使CE=AD,连结AE.
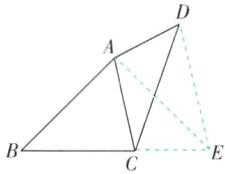
∵∠DAC+∠BCA=180°,∠ACE+∠BCA=180°,
∴∠DAC=∠ECA.在△ADC与△CEA中,{AC=AC,∠DAC=∠ECA,AD=CE,
∴△ADC≌△CEA(SAS),
∴∠ACD=∠CAE,CD=AE.又
∵∠B+∠D=90°,
∴∠BAC+∠ACD=360° - ∠B - ∠D - ∠DAC - ∠BCA=90°,
∴∠BAC+∠CAE=90°,即∠BAE=90°.
∵AB=CD,
∴AB=AE.
∵S△ADC=S△ACE,
∴S四边形ABCD=S△BAE,
∴$\frac{1}{2}$AB·AE=$\frac{1}{2}$CD·CD=18,
∴CD=6(负值已舍去),故答案为6.
6 [解析]如图,延长BC到E,使CE=AD,连结AE.

∵∠DAC+∠BCA=180°,∠ACE+∠BCA=180°,
∴∠DAC=∠ECA.在△ADC与△CEA中,{AC=AC,∠DAC=∠ECA,AD=CE,
∴△ADC≌△CEA(SAS),
∴∠ACD=∠CAE,CD=AE.又
∵∠B+∠D=90°,
∴∠BAC+∠ACD=360° - ∠B - ∠D - ∠DAC - ∠BCA=90°,
∴∠BAC+∠CAE=90°,即∠BAE=90°.
∵AB=CD,
∴AB=AE.
∵S△ADC=S△ACE,
∴S四边形ABCD=S△BAE,
∴$\frac{1}{2}$AB·AE=$\frac{1}{2}$CD·CD=18,
∴CD=6(负值已舍去),故答案为6.
6 [中]如图,在$△AOB$和$△COD$中,$OA = OB,OC = OD,OA < OC,∠AOB = ∠COD = 36^{\circ }$. 连结AC,BD交于点M,连结OM. 下列结论:①$∠AMB = 36^{\circ }$;②$AC = BD$;③OM平分$∠AOD$;④MO平分$∠AMD$.其中正确的结论是 _ .(填序号)
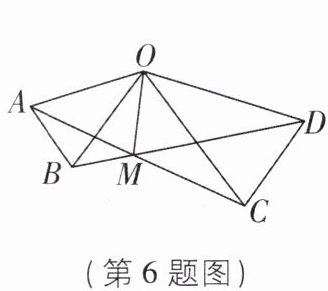

答案:
①②④ [解析]
∵∠AOB=∠COD=36°,
∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD.在△AOC和△BOD中,{OA=OB,∠AOC=∠BOD,OC=OD,
∴△AOC≌△BOD(SAS),
∴∠OAC=∠OBD.
∵∠AMB+∠OBD=∠AOB+∠OAC,
∴∠AMB=∠AOB=36°,
∴①正确.
∵△AOC≌△BOD,
∴AC=BD,
∴②正确.
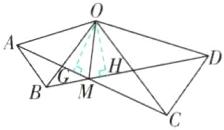
如图,过点O作OG⊥AC于点G,OH⊥BD于点H,则∠OGC=∠OHD=90°.
∵△AOC≌△BOD,
∴∠OCA=∠ODB.在△OCG和△ODH中,{∠OGC=∠OHD,∠OCG=∠ODH,OC=OD,
∴△OCG≌△ODH(AAS),
∴OG=OH.在Rt△OGM和Rt△OHM中,{OM=OM,OG=OH,
∴Rt△OGM≌Rt△OHM(HL),
∴∠OMA=∠OMD,
∴MO平分∠AMD,
∴④正确.由已知无法得到OM平分∠AOD,
∴③错误.综上,正确的结论是①②④,故答案为①②④.
①②④ [解析]
∵∠AOB=∠COD=36°,
∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD.在△AOC和△BOD中,{OA=OB,∠AOC=∠BOD,OC=OD,
∴△AOC≌△BOD(SAS),
∴∠OAC=∠OBD.
∵∠AMB+∠OBD=∠AOB+∠OAC,
∴∠AMB=∠AOB=36°,
∴①正确.
∵△AOC≌△BOD,
∴AC=BD,
∴②正确.

如图,过点O作OG⊥AC于点G,OH⊥BD于点H,则∠OGC=∠OHD=90°.
∵△AOC≌△BOD,
∴∠OCA=∠ODB.在△OCG和△ODH中,{∠OGC=∠OHD,∠OCG=∠ODH,OC=OD,
∴△OCG≌△ODH(AAS),
∴OG=OH.在Rt△OGM和Rt△OHM中,{OM=OM,OG=OH,
∴Rt△OGM≌Rt△OHM(HL),
∴∠OMA=∠OMD,
∴MO平分∠AMD,
∴④正确.由已知无法得到OM平分∠AOD,
∴③错误.综上,正确的结论是①②④,故答案为①②④.
7 [中]如图,已知$AB⊥CD$且$AB = CD$,E,F是AD上两点,$CE⊥AD,BF⊥AD$. 若$AD = 15,CE = 10,BF = 8$,则EF的长为 _ .
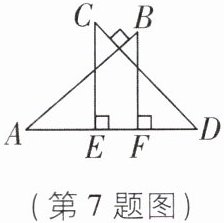

答案:
3 [解析]
∵AB⊥CD,CE⊥AD,
∴∠C+∠D=90°,∠A+∠D=90°,
∴∠A=∠C.
∵CE⊥AD,BF⊥AD,
∴∠AFB=∠CED=90°.在△ABF和△CDE中,{∠AFB=∠CED,∠A=∠C,AB=CD,
∴△ABF≌△CDE(AAS),
∴BF=DE=8,CE=AF=10.
∵AE=AD - DE=15 - 8=7,
∴EF=AF - AE=10 - 7=3.故答案为3.
∵AB⊥CD,CE⊥AD,
∴∠C+∠D=90°,∠A+∠D=90°,
∴∠A=∠C.
∵CE⊥AD,BF⊥AD,
∴∠AFB=∠CED=90°.在△ABF和△CDE中,{∠AFB=∠CED,∠A=∠C,AB=CD,
∴△ABF≌△CDE(AAS),
∴BF=DE=8,CE=AF=10.
∵AE=AD - DE=15 - 8=7,
∴EF=AF - AE=10 - 7=3.故答案为3.
8 [较难]如图,$△ABC$的面积为16,AD平分$∠BAC$,且$AD⊥BD$于点D,则$△ADC$的面积是 _ .
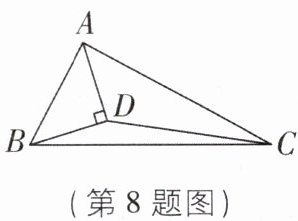

答案:
8 [解析]如图,延长BD交AC于点E.
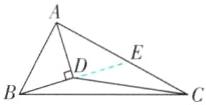
∵AD平分∠BAE,AD⊥BD,
∴∠BAD=∠EAD,∠ADB=∠ADE=90°.在△ABD和△AED中,{∠BAD=∠EAD,AD=AD,∠BDA=∠EDA,
∴△ABD≌△AED(ASA),
∴BD=DE,
∴S△ABD=S△ADE,S△BDC=S△CDE,
∴S△ADC=S△ADE+S△CDE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×16=8.故答案为8.
8 [解析]如图,延长BD交AC于点E.

∵AD平分∠BAE,AD⊥BD,
∴∠BAD=∠EAD,∠ADB=∠ADE=90°.在△ABD和△AED中,{∠BAD=∠EAD,AD=AD,∠BDA=∠EDA,
∴△ABD≌△AED(ASA),
∴BD=DE,
∴S△ABD=S△ADE,S△BDC=S△CDE,
∴S△ADC=S△ADE+S△CDE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×16=8.故答案为8.
9 [中]如图,OC平分$∠AOB$,点P,Q是OC上不同的点,$PE⊥OA,PF⊥OB$,垂足分别为E,F,连结EQ,FQ. 求证:
(1)$△OPE\cong △OPF.$
(2)$FQ = EQ.$
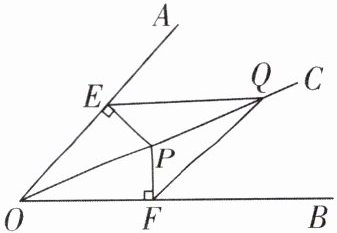
(1)$△OPE\cong △OPF.$
(2)$FQ = EQ.$

答案:
【证明】
(1)
∵OC平分∠AOB,PE⊥OA,PF⊥OB,
∴∠AOC=∠BOC,∠PEO=∠PFO=90°.在△OPE和△OPF中,{∠PEO=∠PFO,∠EOP=∠FOP,OP=OP,
∴△OPE≌△OPF(AAS).
(2)
∵△OPE≌△OPF,
∴OE=OF.在△OEQ和△OFQ中,{OE=OF,∠EOQ=∠FOQ,OQ=OQ,
∴△OEQ≌△OFQ(SAS),
∴EQ=FQ.
(1)
∵OC平分∠AOB,PE⊥OA,PF⊥OB,
∴∠AOC=∠BOC,∠PEO=∠PFO=90°.在△OPE和△OPF中,{∠PEO=∠PFO,∠EOP=∠FOP,OP=OP,
∴△OPE≌△OPF(AAS).
(2)
∵△OPE≌△OPF,
∴OE=OF.在△OEQ和△OFQ中,{OE=OF,∠EOQ=∠FOQ,OQ=OQ,
∴△OEQ≌△OFQ(SAS),
∴EQ=FQ.
查看更多完整答案,请扫码查看


