《2025年初中必刷题八年级数学上册华师大版》

1 [中]代数式 $ yz(xz + 2)-2y(3xz^{2}+z + x)+5xyz^{2} $ 的值( )

A.只与 $ x,y $ 有关
B.只与 $ y,z $ 有关
C.与 $ x,y,z $ 都无关
D.与 $ x,y,z $ 都有关

答案： A 【解析】yz(xz+2)-2y(3xz²+z+x)+5xyz²=xyz²+2yz-6xyz²-2yz-2xy+5xyz²=-2xy,所以代数式的值只与x,y有关.故选A.

2 [中]甲、乙两个长方形的边长如图所示($ m $ 为正整数),其面积分别为 $ S_{1},S_{2} $。若满足条件 $ 0 ＜ n ＜ |S_{1}-S_{2}| $ 的整数 $ n $ 有且只有 8 个,则 $ m $ 为( )


A.4
B.5
C.7
D.8

答案： B 【解析】
∵S₁=(m+7)(m+1)=m²+8m+7,S₂=(m+4)(m+2)=m²+6m+8,
∴S₁-S₂=2m-1.
∵m为正整数,
∴m最小为1,
∴2m-1＞0,
∴|S₁-S₂|=|2m-1|=2m-1.
∵0＜n＜|S₁-S₂|,
∴0＜n＜2m-1.由题意得8＜2m-1≤9,解得$\frac{9}{2}$＜m≤5.
∵m为正整数,
∴m=5.故选B.

3 [2025 河南周口期末,中]已知 $ x - 3y + 2 = 0 $,则 $ 2^{x + y}\cdot4^{y - x}= $______。

答案： 4 【解析】由x-3y+2=0得x-3y=-2,
∴3y-x=2,
∴2^{x+y}·4^{y-x}=2^{x+y}·2^{2y-2x}=2^{x+y+2y-2x}=2^{3y-x}=2²=4.故答案为4.

4 [中]将大小不同的两个正方形按图(1)、图(2)的方式摆放,若图(1)中阴影部分的面积是 20,图(2)中阴影部分的面积是 14,则大正方形的边长是______。

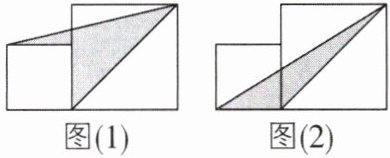
答案： 7 【解析】设大正方形的边长为a,小正方形的边长为b.根据题意可得$\frac{1}{2}$ab+$\frac{1}{2}$b(a-b)=20,$\frac{1}{2}$ab=14,解得a=7,b=4.故答案为7.

5 [较难]观察等式：$ 2 + 2^{2}= 2^{3}-2 $；$ 2 + 2^{2}+2^{3}= 2^{4}-2 $；$ 2 + 2^{2}+2^{3}+2^{4}= 2^{5}-2 $；…。已知按一定规律排列的一组数：$ 2^{50},2^{51},2^{52},…,2^{99},2^{100} $。若 $ 2^{50}= a $,用含 $ a $ 的式子表示这组数的和是______。

答案： 2a²-a 【解析】
∵2+2²=2³-2,2+2²+2³=2⁴-2,2+2²+2³+2⁴=2⁵-2,…,
∴2⁵⁰+2⁵¹+2⁵²+…+2⁹⁹+2¹⁰⁰=(2+2²+2³+…+2⁴⁹)+(2⁵⁰+2⁵¹+2⁵²+…+2⁹⁹+2¹⁰⁰)-(2+2²+2³+…+2⁴⁹)=(2+2²+2³+…+2⁴⁹+2⁵⁰+2⁵¹+2⁵²+…+2⁹⁹+2¹⁰⁰)-(2+2²+2³+…+2⁴⁹)=(2¹⁰¹-2)-(2⁵⁰-2)=2¹⁰¹-2⁵⁰=2·2⁵⁰·2⁵⁰-2⁵⁰.
∵2⁵⁰=a,
∴原式=2·a·a-a=2a²-a,故答案为2a²-a.

6 [2025 海南海口质检,中]尝试解决下列有关幂的问题：
(1)若 $ 3×27^{m}÷9^{m}= 3^{16} $,求 $ m $ 的值；
(2)若 $ 2^{6}= a^{2}= 4^{b} $,求 $ a + b $ 的值；
(3)若 $ n $ 为正整数,且 $ x^{2n}= 4 $,求 $ (3x^{3n})^{2}-4(x^{2})^{2n} $ 的值。

答案： 【解】
(1)
∵3×27ᵐ÷9ᵐ=3¹⁶,
∴3×3³ᵐ÷3²ᵐ=3¹⁶,
∴3¹⁺ᵐ=3¹⁶,
∴1+m=16,
∴m=15.
(2)
∵2⁶=a²=4ᵇ,
∴(2³)²=a²,2⁶=2²ᵇ,
∴a=±2³=±8,2b=6,
∴b=3,
∴a+b=8+3=11或a+b=-8+3=-5.
(3)
∵x²ⁿ=4,
∴(3x³ⁿ)²-4(x²)²ⁿ=9(x²ⁿ)³-4(x²ⁿ)²=9×4³-4×4²=512.

7 [2025 湖南衡阳质检,中]【阅读与思考】
下面是小明同学的数学笔记,请你仔细阅读并完成相应的任务：
对于依次排列的多项式 $ x + a,x + b,x + c,x + d $($ a,b,c,d $ 是常数),当它们满足 $ (x + a)(x + d)-(x + b)(x + c)= M $,且 $ M $ 是常数时,称 $ a,b,c,d $ 是一组“平衡数”,$ M $ 是该组“平衡数”的“平衡因子”。
例：对于依次排列的多项式 $ x + 2,x + 1,x + 6,x + 5 $,
$ \because(x + 2)(x + 5)-(x + 1)(x + 6) $
$ =(x^{2}+7x + 10)-(x^{2}+7x + 6) $
$ =4 $,
$ \therefore2,1,6,5 $ 是一组“平衡数”,4 是该组“平衡数”的“平衡因子”。
【任务一】
(1)已知 6,7,8,9 是一组“平衡数”,求该组“平衡数”的“平衡因子”$ M $ 的值；
【任务二】
(2)若 2,4,$ m $,-9 是一组“平衡数”,求 $ m $ 的值；
【任务三】
(3)当 $ a,b,c,d $ 之间满足怎样的数量关系时,它们是一组“平衡数”？写出它们之间的关系,并说明理由。

答案： 【解】
(1)
∵6,7,8,9是一组“平衡数”,
∴“平衡因子”M=(x+6)(x+9)-(x+7)(x+8)=(x²+9x+6x+54)-(x²+8x+7x+56)=(x²+15x+54)-(x²+15x+56)=x²+15x+54-x²-15x-56=-2,
∴“平衡因子”M=-2.
(2)
∵2,4,m,-9是一组“平衡数”,
∴M=(x+2)(x-9)-(x+4)(x+m)=(x²-9x+2x-18)-(x²+mx+4x+4m)=(x²-7x-18)-(x²+mx+4x+4m)=x²-7x-18-x²-mx-4x-4m=(-11-m)·x-18-4m.
∵M是常数,
∴-11-m=0,解得m=-11.
(3)当a,b,c,d之间满足a+d=b+c时,它们是一组“平衡数”.理由:
∵a,b,c,d是一组“平衡数”,
∴(x+a)(x+d)-(x+b)(x+c)的结果为常数.(x+a)(x+d)-(x+b)(x+c)=(x²+ax+dx+ad)-(x²+bx+cx+bc)=x²+(a+d)x+ad-x²-(b+c)x-bc=[(a+d)-(b+c)]x+(ad-bc).
∵结果为常数,
∴(a+d)-(b+c)=0,
∴a+d=b+c.