第31页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2024 北京通州区期末]下列从左到右的变形属于因式分解的是( )
A.$2x^{2}-2x - 1 = 2x(x - 1)-1$
B.$x^{2}+y^{2}= (x + y)^{2}-2xy$
C.$(a + b)(a - b)= a^{2}-b^{2}$
D.$a^{2}+2a + 1= (a + 1)^{2}$
A.$2x^{2}-2x - 1 = 2x(x - 1)-1$
B.$x^{2}+y^{2}= (x + y)^{2}-2xy$
C.$(a + b)(a - b)= a^{2}-b^{2}$
D.$a^{2}+2a + 1= (a + 1)^{2}$
答案:
D 【解析】A、B、C 选项,等式右边不是乘积的形式,不是因式分解,不符合题意;D 选项,符合因式分解的定义,是因式分解,符合题意.故选 D.
2 [2024 江苏苏州期中]若多项式$x^{2}+mx + 6因式分解得(x + 2)(x + n)$,则$m + n$的值为____。
答案:
8 【解析】
∵(x+2)(x+n)=x²+(2+n)x+2n,
∴2n=6,2+n=m,
∴n=3,m=5,
∴m+n=8,故答案为 8.
∵(x+2)(x+n)=x²+(2+n)x+2n,
∴2n=6,2+n=m,
∴n=3,m=5,
∴m+n=8,故答案为 8.
3 用提公因式法分解$6xy + 8x^{2}y - 4x^{2}yz^{3}$时,提取的公因式是( )
A.$xy$
B.$2xz$
C.$2xy$
D.$3yz$
A.$xy$
B.$2xz$
C.$2xy$
D.$3yz$
答案:
C 【解析】用提公因式法分解6xy+8x²y-4x²yz³时,提取的公因式是2xy.故选 C.
4 [2025 山东烟台招远期末]把多项式$m^{2}(a - 3)+m(3 - a)$分解因式,结果为( )
A.$(a - 3)(m^{2}+m)$
B.$(a - 3)(m^{2}-m)$
C.$m(a - 3)(m - 1)$
D.$m(a - 3)(m + 1)$
A.$(a - 3)(m^{2}+m)$
B.$(a - 3)(m^{2}-m)$
C.$m(a - 3)(m - 1)$
D.$m(a - 3)(m + 1)$
答案:
C 【解析】原式=m²(a-3)-m(a-3)=m(a-3)(m-1),故选 C.
5 长和宽分别为$a$,$b$的长方形,它的周长为$14$,面积为$10$,则$a^{2}b + ab^{2}+ab$的值为( )
A.$2560$
B.$490$
C.$80$
D.$49$
A.$2560$
B.$490$
C.$80$
D.$49$
答案:
C 【解析】
∵长方形的长为a,宽为b,
∴长方形的面积为ab=10,周长为2(a+b)=14,
∴a+b=7,
∴a²b+ab²+ab=ab(a+b+1)=10×(7+1)=80,故选 C.
∵长方形的长为a,宽为b,
∴长方形的面积为ab=10,周长为2(a+b)=14,
∴a+b=7,
∴a²b+ab²+ab=ab(a+b+1)=10×(7+1)=80,故选 C.
6 [2025 四川攀枝花期中]若多项式$(a + b - c)(a + c - b)+(b - a + c)(b - a - c)= M\cdot(a - b + c)$,则多项式$M = $____。
答案:
2(a-c) 【解析】(a+b-c)(a+c-b)+(b-a+c)(b-a-c)=(a+b-c)(a+c-b)-(b-a+c)(a+c-b)=(a+c-b)[(a+b-c)-(b-a+c)]=(a-b+c)(a+b-c-b+a-c)=2(a-c)(a-b+c),
∴M=2(a-c).
∴M=2(a-c).
7 若$a^{2}+a - 1 = 0$,则$a^{2022}+a^{2021}-a^{2020}= $____。
答案:
0 【解析】a²⁰²²+a²⁰²¹-a²⁰²⁰=a²⁰²⁰(a²+a-1).
∵a²+a-1=0,
∴原式=a²⁰²⁰·0=0.故答案为 0.
∵a²+a-1=0,
∴原式=a²⁰²⁰·0=0.故答案为 0.
8 已知$\triangle ABC的三边长a$,$b$,$c满足a^{2}-bc - ab + ac = 0$,则$\triangle ABC$的形状是____。
答案:
等腰三角形 【解析】
∵a²-bc-ab+ac=0,
∴a²-ab-bc+ac=0,
∴(a²-ab)+(ac-bc)=0,
∴a(a-b)+c(a-b)=0,
∴(a-b)(a+c)=0.
∵a+c≠0,
∴a-b=0,
∴a=b,
∴△ABC 是等腰三角形.
∵a²-bc-ab+ac=0,
∴a²-ab-bc+ac=0,
∴(a²-ab)+(ac-bc)=0,
∴a(a-b)+c(a-b)=0,
∴(a-b)(a+c)=0.
∵a+c≠0,
∴a-b=0,
∴a=b,
∴△ABC 是等腰三角形.
9 已知$(2x - 21)(3x - 7)-(3x - 7)(x - 13)可分解因式为(3x + a)(x + b)$,其中$a$,$b$均为整数,则$a + 3b$的值为____。
答案:
-31 【解析】(2x-21)(3x-7)-(3x-7)(x-13)=(3x-7)(2x-21-x+13)=(3x-7)(x-8).
∵(2x-21)(3x-7)-(3x-7)(x-13)可分解因式为(3x+a)(x+b),
∴(3x-7)(x-8)=(3x+a)(x+b),则a=-7,b=-8,
∴a+3b=-7+3×(-8)=-31.故答案为-31.
∵(2x-21)(3x-7)-(3x-7)(x-13)可分解因式为(3x+a)(x+b),
∴(3x-7)(x-8)=(3x+a)(x+b),则a=-7,b=-8,
∴a+3b=-7+3×(-8)=-31.故答案为-31.
10 [2024 山东东营河口区期中]下列各多项式中,能用公式法分解因式的是( )
A.$a^{2}-b^{2}+2ab$
B.$a^{2}+b^{2}+ab$
C.$4a^{2}+12a + 9$
D.$25n^{2}+15n + 9$
A.$a^{2}-b^{2}+2ab$
B.$a^{2}+b^{2}+ab$
C.$4a^{2}+12a + 9$
D.$25n^{2}+15n + 9$
答案:
C 【解析】A、B、D 选项,原式都不能利用公式分解;C 选项,原式=(2a+3)²,符合题意.故选 C.
11 [2025 河北石家庄质检]对于任何整数$m$,多项式$(4m + 5)^{2}-9$都能( )
A.被$8$整除
B.被$m$整除
C.被$(m - 1)$整除
D.被$(2m - 1)$整除
A.被$8$整除
B.被$m$整除
C.被$(m - 1)$整除
D.被$(2m - 1)$整除
答案:
A 【解析】(4m+5)²-9=(4m+5)²-3²=(4m+5+3)(4m+5-3)=(4m+8)(4m+2)=8(m+2)(2m+1),
∴对于任何整数m,多项式(4m+5)²-9都能被8或(m+2)或(2m+1)整除.故选 A.
∴对于任何整数m,多项式(4m+5)²-9都能被8或(m+2)或(2m+1)整除.故选 A.
12 [2025 吉林松原期末]如图,有三种规格的卡片共$9$张,其中边长为$a的正方形卡片4$张,边长为$b的正方形卡片1$张,长、宽分别为$a$,$b的长方形卡片4$张。现使用这$9$张卡片拼成一个大正方形,则这个大正方形的边长为( )
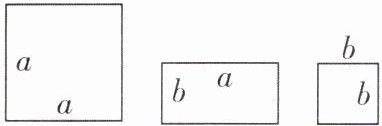
A.$2a + b$
B.$4a + b$
C.$a + 2b$
D.$a + 3b$
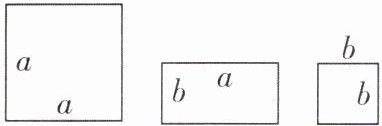
A.$2a + b$
B.$4a + b$
C.$a + 2b$
D.$a + 3b$
答案:
A 【解析】由题意可知,9张卡片总面积为4a²+4ab+b².
∵4a²+4ab+b²=(2a+b)²,
∴大正方形边长为2a+b.故选 A.
∵4a²+4ab+b²=(2a+b)²,
∴大正方形边长为2a+b.故选 A.
13 [2025 山东青岛期末]若$4x^{2}-(k + 1)x + 9$能用完全平方公式分解因式,则常数$k$的值为____。
答案:
-13 或 11 【解析】
∵4x²-(k+1)x+9能用完全平方公式分解因式,
∴-(k+1)=±12,解得k=-13 或 11,故答案为-13 或 11.
∵4x²-(k+1)x+9能用完全平方公式分解因式,
∴-(k+1)=±12,解得k=-13 或 11,故答案为-13 或 11.
14 [2024 重庆南岸区期末]若$x + y = 1$,则$x^{2}-y^{2}+2y + 5= $____。
答案:
6 【解析】
∵x+y=1,
∴x²-y²+2y+5=(x+y)(x-y)+2y+5=x-y+2y+5=x+y+5=6,故答案为 6.
∵x+y=1,
∴x²-y²+2y+5=(x+y)(x-y)+2y+5=x-y+2y+5=x+y+5=6,故答案为 6.
15 (1)因式分解:$6ab^{2}-9a^{2}b - b^{3}$。
(2)因式分解:$(a^{2}+b^{2})^{2}-4a^{2}b^{2}$。
(2)因式分解:$(a^{2}+b^{2})^{2}-4a^{2}b^{2}$。
答案:
【解】
(1)原式=-b(9a²-6ab+b²)=-b(3a-b)².
(2)原式=(a²+b²+2ab)(a²+b²-2ab)=(a+b)²(a-b)².
(1)原式=-b(9a²-6ab+b²)=-b(3a-b)².
(2)原式=(a²+b²+2ab)(a²+b²-2ab)=(a+b)²(a-b)².
16 把$3y^{4}-3x^{4}$分解因式的结果是____。
答案:
3(y²+x²)(y+x)(y-x) 【解析】3y⁴-3x⁴=3(y⁴-x⁴)=3(y²+x²)(y²-x²)=3(y²+x²)(y+x)(y-x).故答案为3(y²+x²)(y+x)(y-x).
查看更多完整答案,请扫码查看


